条件・命題 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
正しい事柄を真、誤りである事柄を偽と言う。
真であるか、偽であるか、そのいずれかを明確に決めることのできる事柄を命題と言う。
命題が偽であることを示す例を反例と言う。
対象となるものの変化の具合によって、真であったり、偽であったりする事柄を条件と言う。条件を表すのに小文字のアルファベットを使います。条件を考えるときには、何を対象としているのかを明示する必要があります。条件cが対象とするもの全体の集合を、条件cの全体集合と言います。
命題が真であるときには、証明することができます。
命題が偽であることを示すためには、反例を1つあげれば十分です。1つでも反例が挙げられる命題は偽だと言えます。
命題は通常、2つの条件c,dについて、「cならばd」という形をしています。このとき、条件cを仮定、条件dを結論と言います。
命題:「cならばd」を記号で、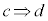 と書きます。
と書きます。
例1.(1) 命題:「xが実数であれば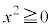 」は、真
」は、真
(2) 命題:「三角形の内角の和は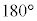 」は、真
」は、真
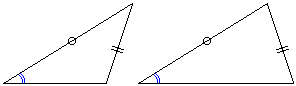 (3) 命題:「2辺と1角が等しい2つの三角形は合同である」は、偽
(3) 命題:「2辺と1角が等しい2つの三角形は合同である」は、偽
反例は右図の2つの三角形。2辺と1角が等しいけれども合同ではありません。
(4) 条件:“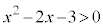 ”は、
”は、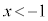 であるか
であるか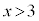 の場合には真ですが、
の場合には真ですが、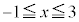 の場合には偽です。
の場合には偽です。
(5) 条件:“xは素数”は、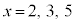 などでは真ですが、
などでは真ですが、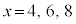 などでは偽です。
などでは偽です。
(6) 条件:“xは奇数”は、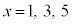 では真ですが、
では真ですが、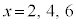 では偽です。
では偽です。
(7) 命題:「“xは素数”であるならば、“xは奇数”」は、偽です。反例は、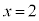
 命題:
命題: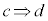 が成り立つとき、つまり真のとき、条件cを満たすものの集合をC,条件dを満たすものの集合をDとすると、この2つの集合の間には右図のような関係があります。条件cを満たすものは、全て条件dを満たすので、集合Cの要素(右図の×点)は全て集合Dの要素であって、集合Cは集合Dに含まれます。つまり、
が成り立つとき、つまり真のとき、条件cを満たすものの集合をC,条件dを満たすものの集合をDとすると、この2つの集合の間には右図のような関係があります。条件cを満たすものは、全て条件dを満たすので、集合Cの要素(右図の×点)は全て集合Dの要素であって、集合Cは集合Dに含まれます。つまり、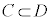 となります。
となります。
 命題:
命題: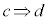 が成り立たないとき、つまり偽のとき、条件cを満たすものの集合をC,条件dを満たすものの集合をDとすると、この2つの集合の間には右図のような関係があります。条件cを満たすものの中に条件dを満たさないものがあるので、集合Cの要素であって集合Dの要素でないもの(これが反例です。右図の×点)が存在します。従って、ベン図は、集合Cが集合Dの外側にはみ出る形になります。反例は、集合
が成り立たないとき、つまり偽のとき、条件cを満たすものの集合をC,条件dを満たすものの集合をDとすると、この2つの集合の間には右図のような関係があります。条件cを満たすものの中に条件dを満たさないものがあるので、集合Cの要素であって集合Dの要素でないもの(これが反例です。右図の×点)が存在します。従って、ベン図は、集合Cが集合Dの外側にはみ出る形になります。反例は、集合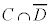 の要素です。
の要素です。
命題: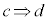 ,命題:
,命題: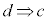 のいずれも真であるとき、”
のいずれも真であるとき、” ”と書きます。条件cを満たすものの集合をC,条件dを満たすものの集合をDとすると、
”と書きます。条件cを満たすものの集合をC,条件dを満たすものの集合をDとすると、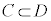 かつ
かつ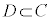 となるので、
となるので、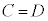 となります。このとき、条件cと条件dとは「同値である」と言います。
となります。このとき、条件cと条件dとは「同値である」と言います。
命題: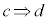 が真であるとき、cをdであるための十分条件、dをcであるための必要条件と言う。
が真であるとき、cをdであるための十分条件、dをcであるための必要条件と言う。
命題: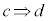 ,命題:
,命題: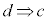 のいずれも真であるとき、つまり、
のいずれも真であるとき、つまり、 であるとき、cはdであるための必要十分条件、dはcであるための必要十分条件と言う。
であるとき、cはdであるための必要十分条件、dはcであるための必要十分条件と言う。
 十分条件は「十分に厳しい条件」であって、満たす範囲が狭い。必要条件は「必要最低限の緩い条件」であって、満たす範囲が広い、ということを、ベン図と合わせてよく理解しておく必要があります。十分条件を満たすものの集合が必要条件を満たすものの集合に含まれるのです(右図)
十分条件は「十分に厳しい条件」であって、満たす範囲が狭い。必要条件は「必要最低限の緩い条件」であって、満たす範囲が広い、ということを、ベン図と合わせてよく理解しておく必要があります。十分条件を満たすものの集合が必要条件を満たすものの集合に含まれるのです(右図)
。
結婚相手を考えるときに、「花婿」の条件に対して、「身長180cm以上、体重65kg以下、大手企業の幹部で年収2000万円以上、自動車あり、家持ち、話題豊富で笑顔が素敵」という条件と、「男」という条件を考えたとします。
「身長180cm以上、体重65kg以下、大手企業の幹部で年収2000万円以上、自動車あり、家持ち、話題豊富で笑顔が素敵」であれば、花婿にしても良いと思うのなら、
「身長180cm以上、体重65kg以下、大手企業の幹部で年収2000万円以上、自動車あり、家持ち、話題豊富で笑顔が素敵」⇒「花婿」
ということになるので、条件:「身長180cm以上、体重65kg以下、大手企業の幹部で年収2000万円以上、自動車あり、家持ち、話題豊富で笑顔が素敵」は、「花婿」であるための十分条件(十分厳しくて、条件を満たすものが少ない、ひょっとしていない?)です。
これでは、婚期を逃してしまうな、と、思うと、男でありさえすれば誰でもいいや、ということにはならないですね。つまり、「男」であっても「花婿」の条件を満たすとは限りません。
「花婿」⇒「男」
ということになるので、「男」であることは、「花婿」であるための必要条件(必要最低限の緩い条件で、何でもござれ)と言うことになります。
例2.(1) “xは実数” ⇔ “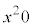 ”は真です。xが実数であることは
”は真です。xが実数であることは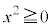 であるための必要十分条件、
であるための必要十分条件、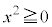 であることはxが実数であるための必要十分条件です。
であることはxが実数であるための必要十分条件です。
(2) “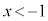 ” ⇒ “
” ⇒ “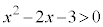 ”は真です。
”は真です。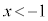 であることは
であることは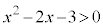 であるための十分条件、
であるための十分条件、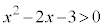 であることは
であることは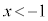 であるための必要条件です。
であるための必要条件です。
(3) 命題:“xが素数” ⇒ “xが奇数”, 命題:“xが奇数” ⇒ “xが素数” は、ともに偽です。“xが素数”であることは、“xが奇数”であるための、必要条件でも十分条件でもありません。同様に、“xが奇数”であることは、“xが素数”であるための必要条件でも十分条件でもありません。
条件cに対して、「cでない」という条件を、条件cの否定と言い、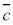 と表す。
と表す。
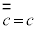 です。
です。
全体集合をUとして、条件c,条件dを満たすものの集合をC,Dとします。
条件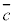 を満たすものの集合は、Cの補集合
を満たすものの集合は、Cの補集合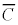 となります。
となります。
“cかつd”を満たすものの集合は、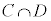 です。
です。
“cまたはd”を満たすものの集合は、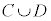 です。
です。
ド・モルガンの法則より、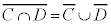 ,
,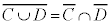
従って、“cかつd”の否定は、“cでないか、またはdでない”となります。
“cまたはd”の否定は、“cでない、かつ、dでない”となります。
つまり、
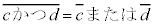 , ,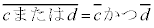 |
否定を作ると、「かつ」が「または」になり、「または」が「かつ」になります。
例3.(1) “xが奇数”の否定は、“xが偶数”です。
(2) “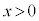 かつ
かつ 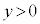 ”の否定は、“
”の否定は、“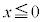 または
または 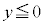 ”です。
”です。
(3) “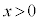 または
または 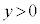 ”の否定は、“
”の否定は、“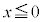 かつ
かつ 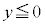 ”です。
”です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。