�@���ʃe�X�g���w IA '21 �N�� 3 ��@ [3] �@���ɂ����������Ă��锠����������A�e���̊O���͓����ł��邪�A�����肭���������m���͈قȂ��Ă���B���������̌��ʂ���A�ǂ̔����炭�����������\�������������A�����t���m����p���čl���悤�B
(1) �����肭���������m���� A �ƁA�����肭���������m���� B �̓�̔��̏ꍇ���l����B (i) �e���ŁA������ 1 �{�����Ă͂��Ƃɖ߂����s�� 3 ��J��Ԃ����Ƃ�
�� A �ɂ����āA 3 ���傤�� 1 ����m���� �� B �ɂ����āA 3 ���傤�� 1 ����m���� �ł���B
(ii) �܂��A A �� B �̂ǂ��炩����̔����ł���߂ɑI�ԁB���ɂ��̑I���ɂ����āA������ 1 �{�����Ă͂��Ƃɖ߂����s�� 3 ��J��Ԃ����Ƃ���A 3 ���傤�� 1 �������B���̂Ƃ��A�� A ���I��鎖�ۂ� A �C�� B ���I��鎖�ۂ� B �C 3 ���傤�� 1 ���鎖�ۂ� W �Ƃ����
�C �ł���B 3 ���傤�� 1 �������Ƃ��A�I���� A �ł�������t���m�� (2) (1) �� ( �� ) �����藧�B ���� ( �� ) �F �̉Q �@�a�@�@ 2 ��̘a�@�@ 3 ��̘a�@�@ (3) �Ԏq����Ƒ��Y��������� ( �� ) �ɂ��Ęb���Ă���B
�Ԏq�F���� ( �� ) �͂Ȃ����藧�̂��ȁH
���Y�F �Ԏq�F�Ȃ�قǂˁB�O���������O�̔��̏ꍇ�́A������ �����肭���������m�����A A �A B �C C �̎O�̔��̏ꍇ���l����B�܂��A A �C B �C C �̂����ǂꂩ����ł���߂ɑI�ԁB���ɂ��̑I���ɂ����āA������ 1 �{�����Ă͂��Ƃɖ߂����s�� 3 ��J��Ԃ����Ƃ���A 3 ���傤�� 1 �������B���̂Ƃ��A�I���� A �ł�������t���m���� (4)
�Ԏq�F�ǂ���甠���O�̏ꍇ�ł��A�����t���m���� 3 ���傤�� 1 ���肭���������m���� ���Y�F�������ˁB����𗘗p����ƁA�����t���m���̒l�͌v�Z���Ȃ��Ă��A���̑傫�����r���邱�Ƃ��ł���ˁB
�����肭���������m�����A A �C B �C C �C D �̎l�̔��̏ꍇ���l����B�܂��A A �C B �C C �C D �̂����ǂꂩ��̔����ł���߂ɑI�ԁB���ɂ��̑I���ɂ����āA������ 1 �{�����Ă͂��Ƃɖ߂����s�� 3 ��J��Ԃ����Ƃ���A 3 �� 1 �������B���̂Ƃ��A�����t���m����p���āA�ǂ̔����炭�����������\�������������l����B�\�������������珇�ɕ��ׂ�� �@ A �C B �C C �C D �@�@ A �C B �C D �C C �@�@ A �C C �C B �C D �@ A �C C �C D �C B �@�@ A �C D �C B �C C �@�@ B �C A �C C �C D �@ B �C A �C D �C C �@�@ B �C C �C A �C D �@�@ B �C C �C D �C A �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� �^�����Ɏ��g�ނ̂ł͂ƂĂ����Ԃ�����܂���B�����t���m���̈Ӗ����킩���Ă���A�q���g�����Ă���̂ŁA�v�Z�Ɏ��Ԃ�����邱�Ƃ͂Ȃ��͂��ł��B (1)(i) �� A �ɂ����āA 3 ���傤�� 1 ����m���́A�������s�̌������A
�A�@ 3 �@�C�@ 8 ......[ �� ] �� B �ɂ����āA 3 ���傤�� 1 ����m���́A
�E�@ 4 �@�G 9 ......[ �� ]
(ii) �I���� A �ł�������t���m�� �I�J�@ 27 �@�L�N�@ 59 ......[ �� ]
�P�R�@ 32 �@�T�V�@ 59 ......[ �� ]
(2) �� A ��I�Ԋm���Ɣ� B ��I�Ԋm���͂Ƃ��� �܂�A 3 ......[ �� ] (3) �� C �ɂ����āA 3 ���傤�� 1 ����m���́A
�e���̊O���͓����ŁA�� A �C�� B �C�� C ��I�Ԋm���͓������A�Ԏq����̌��t�ɂ���q���g���A 3 ���傤�� 1 �������Ƃ��A�I�����A�� A �C�� B �C�� C �ł���m���́A�e���ɂ����āA 3 ���傤�� 1 ����m���̔�A 216 �F 256 �F 243 �@����B�@�ɓ������A�I������ A �ł���m���́A 216 �@�`�c�e�@ 715 ......[ �� ] (4) �� D �ɂ����āA 3 ���傤�� 1 ����m���́A
3 ���傤�� 1 ����m���́A�B���A�傫������ B �C C �C A �ł��B D �� C �� A �̊Ԃɓ���܂��B����āA�\�������������珇�ɁA B �C C �C D �C A �g�@ 8 ......[ �� ] �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@ ���w TOP �@�@ TOP �y�[�W�ɖ߂� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B �e���̒��쌠�� © 2005-2024 (�L)����� ��w�y�w�m ���������t���I ���n��w�l�b�g�m ��w�y�w�m (���ē��������� )������́A������܂Ń��[�� ��  �@����@
�@����@ �@����A
�@����A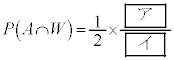 �C
�C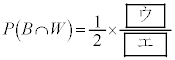
 �ƂȂ�B�܂��A�����t���m��
�ƂȂ�B�܂��A�����t���m�� �ƂȂ�B
�ƂȂ�B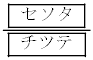 �ƂȂ�B
�ƂȂ�B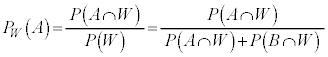
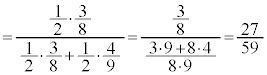
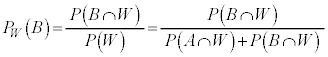
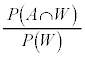 �F
�F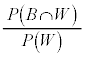 ���@�F�A
���@�F�A