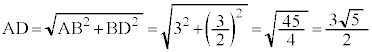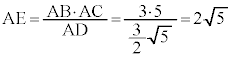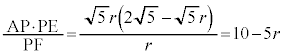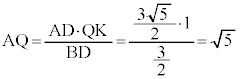共通テスト数学IA '21年第5問
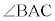 の二等分線と辺BCとの交点をDとすると
の二等分線と辺BCとの交点をDとすると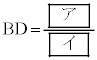 ,
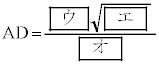
,
である。
また、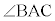 の二等分線と△ABCの外接円Oとの交点で点Aとは異なる点をEとする。△AECに着目すると、
の二等分線と△ABCの外接円Oとの交点で点Aとは異なる点をEとする。△AECに着目すると、 である。
△ABCの2辺ABとACの両方に接し、外接円Oに内接する円の中心をPとする。円Pの半径をrとする。さらに、円Pと外接円Oとの接点をFとし、直線PFと外接円Oとの交点で点Fとは異なる点をGとする。このとき、
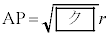 ,
,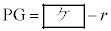
と表せる。したがって、方べきの定理により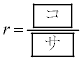 である。
である。
△ABCの内心をQとする。内接円Qの半径は で、
で、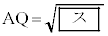 である。また、円Pと辺ABとの接点をHとすると、
である。また、円Pと辺ABとの接点をHとすると、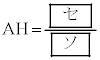 である。
である。
以上から、点Hに関する次の(a),(b)の正誤の組み合わせとして正しいものは である。
である。 (a) 点Hは3点B,D,Qを通る円の周上にある。
(b) 点Hは3点B,E,Qを通る円の周上にある。
 の解答群
の解答群
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 センター試験の平面図形の問題と変わり映えしません。途中、解答欄の形からエによってキ、ク、ス、またケは答がわかってしまいます。根号内の整数が1種類にならないように、など、出題者には、もう一段の工夫を望みたいところです。
ADが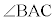 の二等分線であることから、AB:AC = BD:DC = 3:5
の二等分線であることから、AB:AC = BD:DC = 3:5
よって、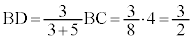
ア 3 イ 2 ......[答]
三平方の定理より、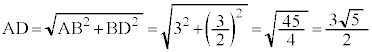
ウ 3 エ 5 オ 2 ......[答]
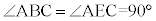 (直径の上に立つ円周角),
(直径の上に立つ円周角),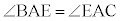 より、△ABD ∽ △AEC ∴ AB:AD = AE:AC
より、△ABD ∽ △AEC ∴ AB:AD = AE:AC
カ 2 キ 5 ......[答]
HP // BDより、AP:PH = AD:BD = 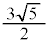 :
: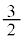 =
= 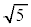 :1
:1
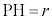 より、
より、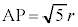
ク 5 ......[答]
点Fは、円Pと外接円Oとの接点なので、FGは外接円Oの直径で、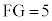
よって、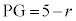
ケ 5 ......[答]
一方、方べきの定理より、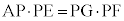
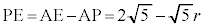 ,
,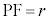 より
より
よって、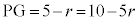 ∴
∴ 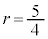
コ 5 サ 4 ......[答]
内接円Qの半径をRとして、
△ABC = △ABQ+△BCQ+△CAQ
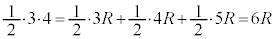 ∴
∴ 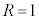
内接円Qと辺ABとの接点をKとすると、△AKQ ∽ △ABD
∴ 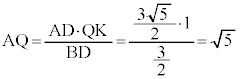
ス 5 ......[答]
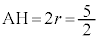
セ 5 ソ 2 ......[答]
従って、AH:AQ = AD:AB,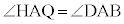 より、△AHQ ∽ △ADB
より、△AHQ ∽ △ADB
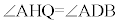 より、四角形BDQHは円に内接する四角形です。一方、Q,D,Eは一直線上に存在するため(円と直線が異なる3点で交わることはない)、四角形BEQHは円に内接しません。
より、四角形BDQHは円に内接する四角形です。一方、Q,D,Eは一直線上に存在するため(円と直線が異なる3点で交わることはない)、四角形BEQHは円に内接しません。
タ 1 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  ,
,
 である。
である。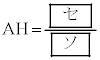 である。
である。