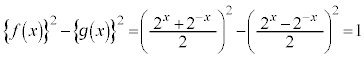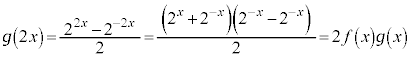�@���ʃe�X�g���wIIB '21�N��1��@
[1](1) �������A�ɂ��čl���悤
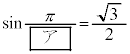 �C
�C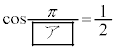
�ł��邩��A�O�p���̍����ɂ��
�ƕό`�ł���B����āAy��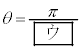 �ōő�l
�ōő�l ���Ƃ�B
���Ƃ�B (2) p��萔�Ƃ��A�������B�ɂ��čl���悤�B
(ii) 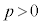 �̂Ƃ��́A���@�藝
�̂Ƃ��́A���@�藝 ��p�����
�ƕ\�����Ƃ��ł���B�������Aα��
�������̂Ƃ���B���̂Ƃ��Ay��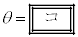 �ōő�l
�ōő�l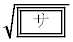 ���Ƃ�B
���Ƃ�B (iii) 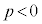 �̂Ƃ��Ay��
�̂Ƃ��Ay��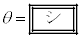 �ōő�l
�ōő�l ���Ƃ�B
���Ƃ�B 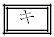 �`
�` �C
�C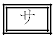 �C
�C �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B) �@
�@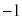 �@�@
�@�@ �@1�@�@
�@1�@�@ �@
�@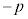
 �@p�@�@
�@p�@�@ �@
�@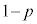 �@�@
�@�@ �@
�@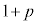
 �@
�@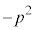 �@�@
�@�@ �@
�@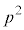 �@�@
�@�@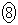 �@
�@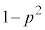
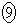 �@
�@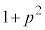 �@�@
�@�@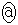 �@
�@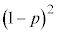 �@�@
�@�@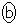 �@
�@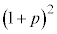
 �C
�C �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B)
[2]�@��̊�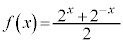 �C
�C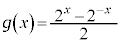 �ɂ��čl����B
�ɂ��čl����B (1) 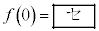 �C
�C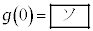 �ł���B�܂��A
�ł���B�܂��A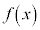 �͑������ςƑ��敽�ς̊W����A
�͑������ςƑ��敽�ς̊W����A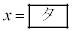 �ōŏ��l
�ōŏ��l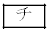 ���Ƃ�B
���Ƃ�B 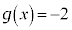 �ƂȂ�x�̒l��
�ƂȂ�x�̒l�� �ł���B
�ł���B(2) ���̇@�`�C�́Ax�ɂǂ̂悤�Ȓl�������Ă��˂ɐ��藧�B
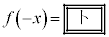 �@����@
�@����@
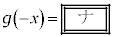 �@����A
�@����A
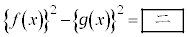 �@����B
�@����B
 �@����C
�@����C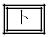 �C
�C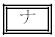 �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B)(3) �Ԏq����Ƒ��Y����́A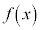 ��
��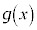 �̐����ɂ��Ęb���Ă���B
�̐����ɂ��Ęb���Ă���B �Ԏq�F�@�`�C�͎O�p���̐����Ɏ��Ă���ˁB
���Y�F�O�p���̉��@�藝�ɗގ�������(A)�`(D)���l���Ă݂����ǁA�˂ɐ��藧���͂��邾�낤���B
�Ԏq�F���藧���Ȃ����������邽�߂ɁA��(A)�`(D)��β�ɉ�����̓I�Ȓl�������Ē��ׂĂ݂���ǂ����ȁB
���Y���l������
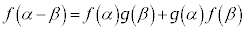 �@���(A)
�@���(A)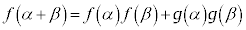 �@���(B)
�@���(B)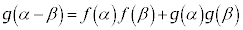 �@���(C)
�@���(C)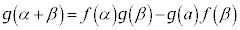 �@���(D)
�@���(D)(1)�C(2)�Ŏ����ꂽ���Ƃ̂������𗘗p����ƁA��(A)�`(D)�̂����A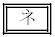 �ȊO�̎O�͐��藧���Ȃ����Ƃ��킩��B
�ȊO�̎O�͐��藧���Ȃ����Ƃ��킩��B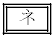 �͍��ӂƉE�ӂ����ꂼ��v�Z���邱�Ƃɂ���Đ��藧���Ƃ��m���߂���B
�͍��ӂƉE�ӂ����ꂼ��v�Z���邱�Ƃɂ���Đ��藧���Ƃ��m���߂���B
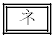 �̉Q
�̉Q  �@(A)�@�@
�@(A)�@�@ �@(B)�@�@
�@(B)�@�@ �@(C)�@�@
�@(C)�@�@ �@(D)
�@(D)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Z���^�[�����������Ȃ�v�Z�y�߂ň�ʂ��b�����̗�����₤���e�ŁA�ǂ��X�����Ǝv���܂��B
[1](1) 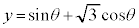 (
(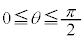 )
) 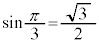 �C
�C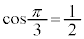
�A�@3 ......[��]�O�p���̍����ɂ��A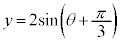
�C�@2 ......[��]
y�́A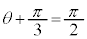 �C�܂�A
�C�܂�A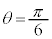 �̂Ƃ��A�ő�l2�E�@6�@�G�@2 ......[��]
�̂Ƃ��A�ő�l2�E�@6�@�G�@2 ......[��] (2) ��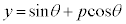 (
(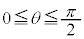 )
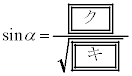
) (i) 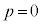 �̂Ƃ��A
�̂Ƃ��A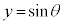 ��
��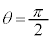 �ōő�l1���Ƃ�܂��B
�ōő�l1���Ƃ�܂��B �I�@2�@�J�@1 ......[��]
(ii) 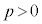 �̂Ƃ��A
�̂Ƃ��A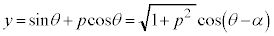
α�́A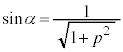 �C
�C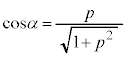 �C
�C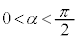
�L�@9�@�N�@1�@�P�@3 ......[��]
y�́A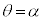 �ōő�l
�ōő�l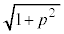 ���Ƃ�B
���Ƃ�B
�R�@1�@�T�@9 ......[��] 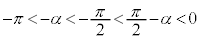 �Ȃ̂ŁA
�Ȃ̂ŁA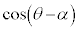 �A���Ȃ킿y�́A
�A���Ȃ킿y�́A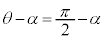 �܂�
�܂�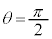 �̂Ƃ��A�ő�l
�̂Ƃ��A�ő�l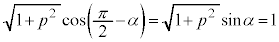 ���Ƃ�܂��B
���Ƃ�܂��B�V�@2�@�X�@1 ......[��]
[2]�@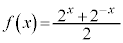 �C
�C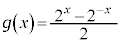
(1) 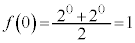 �C
�C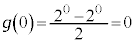
�Z�@1�@�\�@0 ......[��]�������ρE���敽�ς̊W���A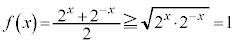 �C���������́A
�C���������́A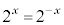 �܂�A
�܂�A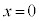 �̂Ƃ��B
�̂Ƃ��B
�^�@0�@�`�@1 ......[��]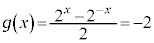 �Ƃ���ƁA
�Ƃ���ƁA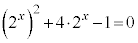 �@��
�@�� 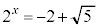 (
(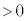 )����āA
)����āA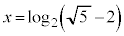
�c�@5�@�e�@2 ......[��] (2) 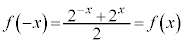
�g�@0 ......[��]
�i�@3 ......[��]
�j�@1 ......[��]
�k�@2 ......[��]
(3) (A)�C(B)�C(C)�C(D)��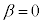 �Ƃ���ƁA
�Ƃ���ƁA 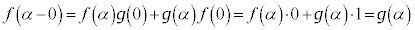 �@�s�����B
�@�s�����B
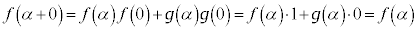 �@�����B
�@�����B
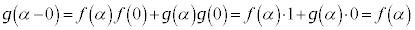 �@�s�����B
�@�s�����B
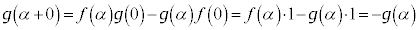 �@�s�����B
�@�s�����B
�l�@1 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 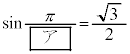 �C
�C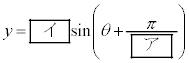
 �C
�C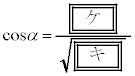 �C
�C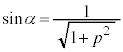 �C
�C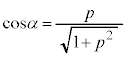 �C
�C