���嗝�n���w'20�N�O��[2]
p�𐳂̐����Ƃ���Bα�Cβ��x�Ɋւ��������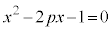 ��2�̉��ŁA
��2�̉��ŁA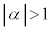 �ł���Ƃ���B
�ł���Ƃ���B
(1) ���ׂĂ̐��̐���n�ɑ��A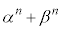 �͐����ł���A����ɋ����ł��邱�Ƃ��ؖ�����B
�͐����ł���A����ɋ����ł��邱�Ƃ��ؖ�����B (2) �Ɍ�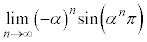 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���嗝�n2003�N[4]�̗ޑ�ł��B(1)�́A3���ԑQ�����̈�ʍ��������������̉�s�Ct��p���āA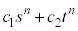 �̌`(
�̌`(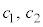 �͒萔)�ɕ\���邱�Ƌy�����w�I�A�[�@��p�����^�p�^�[���̖��ƌ����Ă��悢�̂ŁA�̗�����L�����Ă��܂����炢�ł悢�ł��傤�B(2)��
�͒萔)�ɕ\���邱�Ƌy�����w�I�A�[�@��p�����^�p�^�[���̖��ƌ����Ă��悢�̂ŁA�̗�����L�����Ă��܂����炢�ł悢�ł��傤�B(2)��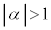 �Ȃ̂�
�Ȃ̂�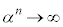 �ƂȂ�A���̂܂܂ł͍l���ɂ����̂ł����A
�ƂȂ�A���̂܂܂ł͍l���ɂ����̂ł����A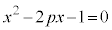 ��2��α�Cβ�ɂ��āA2���������̉��ƌW���̊W���
��2��α�Cβ�ɂ��āA2���������̉��ƌW���̊W���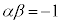 �C
�C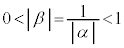 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA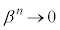 �𗘗p���邱�ƂɂȂ�܂��B
�𗘗p���邱�ƂɂȂ�܂��B
���āA2���������̉��ƌW���̊W���A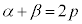 �C
�C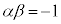 �@����@
�@����@
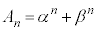 �Ƃ��܂��B
�Ƃ��܂��B
(1) (�T) 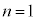 �̂Ƃ��Ap�����̐����ł��邱�Ƃ���A
�̂Ƃ��Ap�����̐����ł��邱�Ƃ���A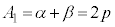 �́A�����ł�������ł��B����āA�������܂��B
�́A�����ł�������ł��B����āA�������܂��B (�U) 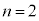 �̂Ƃ��A�@��p���āA
�̂Ƃ��A�@��p���āA 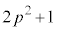 �͐����Ȃ̂ŁA
�͐����Ȃ̂ŁA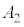 �͐����ł�������ł��B����āA�������܂��B
�͐����ł�������ł��B����āA�������܂��B(�V) 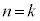 �̂Ƃ��A
�̂Ƃ��A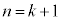 �̂Ƃ��A��������Ɖ��肵�܂��B�܂�A
�̂Ƃ��A��������Ɖ��肵�܂��B�܂�A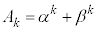 �C
�C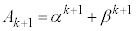 �������ł���������Ɖ��肵�܂��B
�������ł���������Ɖ��肵�܂��B ��蕶��2����������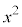 �̑����
�̑����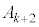 �Cx�̑����
�Cx�̑����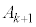 �C�萔����萔����
�C�萔����萔����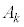 �����������̂������������l���܂��B
�����������̂������������l���܂��B 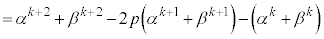
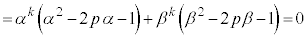 �@(��@α�Cβ��2��������
�@(��@α�Cβ��2��������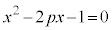 �̉�)
�̉�)����āA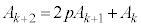 ���܂��A�����ł�������ł��B����āA
���܂��A�����ł�������ł��B����āA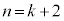 �̂Ƃ����������܂��B
�̂Ƃ����������܂��B (�T)�C(�U)�C(�V)���A���w�I�A�[�@�ɂ���āA���ׂĂ̐��̐���n�ɑ��A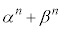 �͐����ł�������ł��B�@(�ؖ��I)
�͐����ł�������ł��B�@(�ؖ��I)
(2) 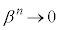 �𗘗p���邽�߂ɁA
�𗘗p���邽�߂ɁA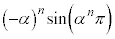 ��
��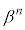 ���g���ĕ\�����Ƃ��l���܂��B
���g���ĕ\�����Ƃ��l���܂��B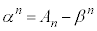 ���A
���A
(1)���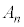 �͋����Ȃ̂ŁA
�͋����Ȃ̂ŁA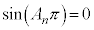 �C
�C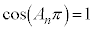 �C����āA
�C����āA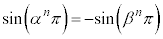
�����ŁA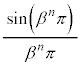 (
(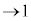 )�̌`(�Ɍ��̌������Q��)���o�Ă���悤�ɕό`���܂��B
)�̌`(�Ɍ��̌������Q��)���o�Ă���悤�ɕό`���܂��B �@���A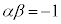 �C
�C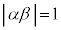 ���A
���A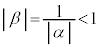 �C����āA
�C����āA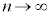 �̂Ƃ��A
�̂Ƃ��A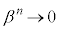 �C
�C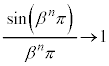
������A 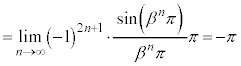 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
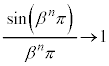
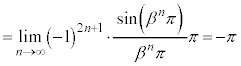 ......[��]
......[��]