単調増加関数,単調減少関数 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
関数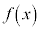 について、2実数a,bが、
について、2実数a,bが、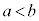 であるとき、
であるとき、
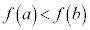 であれば、
であれば、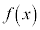 を単調増加関数
を単調増加関数
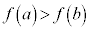 であれば、
であれば、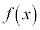 を単調減少関数
を単調減少関数
という。
[例] 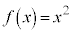 は、
は、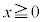 において、
において、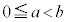 であれば、
であれば、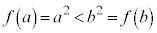 より単調増加
より単調増加
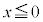 において、
において、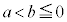 であれば、
であれば、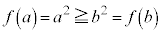 (
(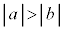 )より単調減少
)より単調減少
区間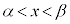 (開区間といい、
(開区間といい、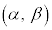 と書く)において、微分可能な関数
と書く)において、微分可能な関数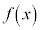 に関して以下のことが成り立つ。
に関して以下のことが成り立つ。
区間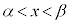 において、
において、
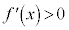 ならば、
ならば、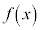 は単調増加関数
は単調増加関数
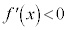 ならば、
ならば、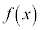 は単調減少関数
は単調減少関数
[証明] 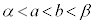 となるように2実数a,bをとる。
となるように2実数a,bをとる。
平均値の定理より、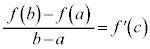 ,
,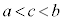 なる実数cが存在する。
なる実数cが存在する。
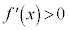 であれば
であれば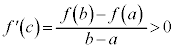 だから、
だから、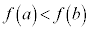
よって、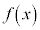 は単調増加関数。
は単調増加関数。
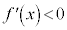 であれば
であれば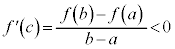 だから、
だから、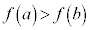
よって、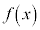 は単調減少関数。
は単調減少関数。
[注意] 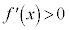 という条件を
という条件を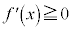 にゆるめると、
にゆるめると、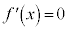 となる区間では関数の値が一定になる。
となる区間では関数の値が一定になる。
このとき、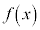 は(減少しないという意味で)広義の単調増加という。
は(減少しないという意味で)広義の単調増加という。
但し、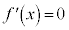 となるxを
となるxを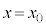 として、
として、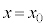 のすぐ近くの周辺(近傍という)で、
のすぐ近くの周辺(近傍という)で、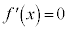 となるxが他になければ、
となるxが他になければ、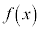 は単調増加になる。
は単調増加になる。
同様に、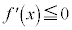 のとき、
のとき、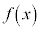 は広義の単調減少で、
は広義の単調減少で、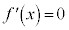 となるxの近傍で
となるxの近傍で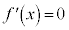 となるxが他になければ、
となるxが他になければ、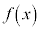 は単調減少になる。
は単調減少になる。
[例] 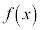 が
が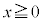 において微分可能でかつ
において微分可能でかつ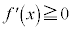 ならば、
ならば、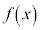 は広義の単調増加で、
は広義の単調増加で、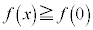
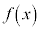 が
が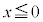 において微分可能でかつ
において微分可能でかつ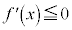 ならば、
ならば、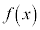 は広義の単調減少で、
は広義の単調減少で、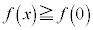
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。