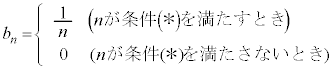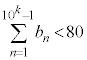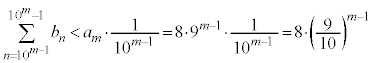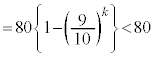���H�吔�w'21�N�O��[1]
���̐����Ɋւ������
(��)�@10�i�@�ŕ\�����Ƃ��ɁA�ǂ̈ʂɂ�����9������Ȃ�
���l����B�ȉ��̖₢�ɓ�����B
(1) k�𐳂̐����Ƃ���Ƃ��A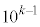 �ȏォ��
�ȏォ��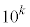 �����ł����ď���(��)�������̐����̌���
�����ł����ď���(��)�������̐����̌���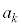 �Ƃ���B���̂Ƃ��A
�Ƃ���B���̂Ƃ��A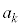 ��k�̎��ŕ\���B
��k�̎��ŕ\���B (2) ���̐���n�ɑ��āA
�Ƃ����B���̂Ƃ��A���ׂĂ̐��̐���k�ɑ��Ď��̕s���������藧���Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)��(2)�̃q���g�ɂȂ��Ă��܂��B�ׂ����l�����܂��ɁA�y�����������ōs���܂��傤�B
(1) 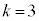 ���炢�ŋ�̓I�ɍl���Ă݂܂��B
���炢�ŋ�̓I�ɍl���Ă݂܂��B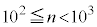 ��������n�́A3���̐����ŁA�ǂ̈ʂɂ�����9������Ȃ��̂́A
��������n�́A3���̐����ŁA�ǂ̈ʂɂ�����9������Ȃ��̂́A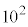 �̈ʂ�1�`8��8�ʂ�A
�̈ʂ�1�`8��8�ʂ�A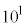 �̈ʂ�0�`8��9�ʂ�C10�̈ʂ�0�`8��9�ʂ�ŁA(��)���������́A
�̈ʂ�0�`8��9�ʂ�C10�̈ʂ�0�`8��9�ʂ�ŁA(��)���������́A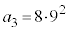 ����܂��B
����܂��B 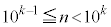 �C���A����(��)�������̐���n�́A���l�ɂ��āA
�C���A����(��)�������̐���n�́A���l�ɂ��āA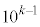 �̈ʂ̐�����1�`8��8�ʂ�A
�̈ʂ̐�����1�`8��8�ʂ�A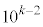 �̈ʂ���
�̈ʂ���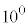 �̈ʂ܂ł�
�̈ʂ܂ł�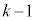 ���̐����ɂ���0�`8��9�ʂ肸����̂ŁA
���̐����ɂ���0�`8��9�ʂ肸����̂ŁA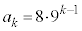 .....[��]
.....[��](2) (1)�̍l�������g���āA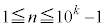 �͈̘̔͂a���A
�͈̘̔͂a���A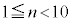 �C
�C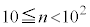 �C
�C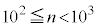 �C����C
�C����C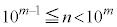 �C����C
�C����C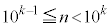 �ɕ����čl���܂��B�����A
�ɕ����čl���܂��B�����A 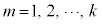 �Ƃ��āA
�Ƃ��āA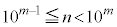 �C���A����(��)����
�C���A����(��)����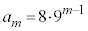 �̐���n�ɂ��āA
�̐���n�ɂ��āA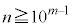 ���A
���A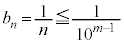 �C����āA
�C����āA����āA�@���A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B