���H�吔�w'21�N�O��[2]
xy���ʏ�̑ȉ~
E�F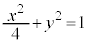
�ɂ��āA�ȉ��̖₢�ɓ�����B
(1) a�Cb�������Ƃ���B����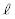 �F
�F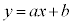 �Ƒȉ~E���قȂ�2�_�����L���邽�߂�a�Cb�̏��������߂�B
�Ƒȉ~E���قȂ�2�_�����L���邽�߂�a�Cb�̏��������߂�B (2) ����a�Cb�Cc�ɑ��āA����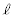 �F
�F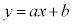 �ƒ���m�F
�ƒ���m�F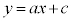 �����ꂼ��ȉ~E�ƈقȂ�2�_�����L���Ă���Ƃ���B�������A
�����ꂼ��ȉ~E�ƈقȂ�2�_�����L���Ă���Ƃ���B�������A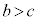 �Ƃ���B����
�Ƃ���B����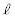 �Ƒȉ~E��2�̋��L�_�̂���x���W�̏���������P�C�傫������Q�Ƃ���B�܂��A����m�Ƒȉ~E��2�̋��L�_�̂���x���W�̏���������S�C�傫������R�Ƃ���B���̂Ƃ��A����
�Ƒȉ~E��2�̋��L�_�̂���x���W�̏���������P�C�傫������Q�Ƃ���B�܂��A����m�Ƒȉ~E��2�̋��L�_�̂���x���W�̏���������S�C�傫������R�Ƃ���B���̂Ƃ��A���� �����藧���߂�a�Cb�Cc�̏��������߂�B
(3) �ȉ~E���4�_�̑g�ŁA������4���_�Ƃ���l�p�`�������`�ł�����̂����ׂċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�f���ɂ���čs����(3)�ŁA�����H�Ƃ������Ƃ��N���܂��B��Ò����ɐ蔲���܂��傤�B
(1) �ȉ~E�̕�����������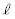 �̕�������A������ƁA
�̕�������A������ƁA �ȉ~E�ƒ���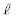 ���قȂ�2�_�����L����̂ŁA�@�����ʎ��́A
���قȂ�2�_�����L����̂ŁA�@�����ʎ��́A ���߂�����́A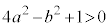 ......[��]�@����A
......[��]�@����A (2) 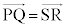 �Ƃ��������ł����A����
�Ƃ��������ł����A����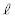 �ƒ���m�͌X�����������̂ŁA
�ƒ���m�͌X�����������̂ŁA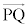 ��
��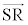 �͕��s�ł��B�]���āA
�͕��s�ł��B�]���āA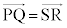 �ƂȂ邽�߂ɂ́A
�ƂȂ邽�߂ɂ́A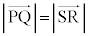 ���K�v�ł��B�v����ɁA
���K�v�ł��B�v����ɁA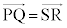 �Ƃ������Ƃ́A�l�p�`PQRS�����s�l�ӌ`�A�Ƃ������Ƃł��B
�Ƃ������Ƃ́A�l�p�`PQRS�����s�l�ӌ`�A�Ƃ������Ƃł��B �ȉ~E�ƒ���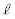 �̋��L�_P�CQ��x���W
�̋��L�_P�CQ��x���W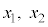 (
(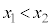 )�́A�������@�̉�(2�����������Q��)�ŁA�����A�̂��ƂɁA
)�́A�������@�̉�(2�����������Q��)�ŁA�����A�̂��ƂɁA �ȉ~E�̕������ƒ���m�̕�������A������ƁA�@��b��c�ɓ���ւ��āA
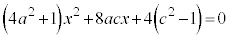 �@����B
�@����B�ȉ~E�ƒ���m���قȂ�2�_�����L����̂ŁA�B�̔��ʎ��́A
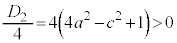 �@��
�@�� 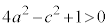 �@����C
�@����C�ȉ~E�ƒ���m�̋��L�_S�CR��x���W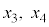 (
(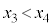 )�́A�������B�̉��ŁA�����C�̂��ƂɁA
)�́A�������B�̉��ŁA�����C�̂��ƂɁA 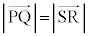 ���A
���A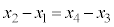
����āA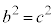 �C
�C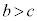 ���A
���A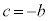 ����
����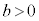 �C���̂Ƃ��A�ƇC�͓��������ɂȂ�܂��B
�C���̂Ƃ��A�ƇC�͓��������ɂȂ�܂��B
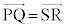 �����藧���߂̏����́A
�����藧���߂̏����́A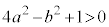 ����
����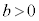 ����
����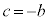 ......[��]���̂Ƃ��A
......[��]���̂Ƃ��A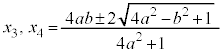 �@(�����́{��
�@(�����́{��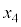 �C�|��
�C�|��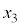 )
) (3) (2)�̎l�p�`PQRS�������`�ɂȂ邽�߂ɂ́A(2)�̏����ɉ����āA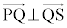 ����
����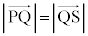
Q�CS��y���W��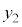 �C
�C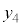 �Ƃ���ƁAQ�CS�́A����
�Ƃ���ƁAQ�CS�́A����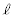 �C����m��̓_�Ȃ̂ŁA
�C����m��̓_�Ȃ̂ŁA ����PQ�̌X���ƒ���QS�̌X���̐ς́A
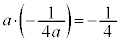 �@����D
�@����D����ł́A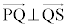 �ƂȂ蓾�܂���I(2�����̕��s�Ɛ������Q��)�ł����A�����̌X�����Aa�Ƃ�
�ƂȂ蓾�܂���I(2�����̕��s�Ɛ������Q��)�ł����A�����̌X�����Aa�Ƃ�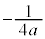 �Ƃ����悤�Ȍ`�ɕ\���Ȃ����������蓾�܂��Bx���ɐ����Ȓ����ł��B�܂�ȉ~E�ƒ���
�Ƃ����悤�Ȍ`�ɕ\���Ȃ����������蓾�܂��Bx���ɐ����Ȓ����ł��B�܂�ȉ~E�ƒ���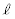 �C����m�̌�_�Ő����`���ł��Ȃ��Ă��Ax���ɕ��s�Ȓ�����x���ɐ����Ȓ����ƂŐ����`���ł��Ȃ����l���܂��Bx���ɕ��s�Ȓ����́A
�C����m�̌�_�Ő����`���ł��Ȃ��Ă��Ax���ɕ��s�Ȓ�����x���ɐ����Ȓ����ƂŐ����`���ł��Ȃ����l���܂��Bx���ɕ��s�Ȓ����́A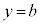 �ƕ\����܂��BE�̕������ɑ�����āA
�ƕ\����܂��BE�̕������ɑ�����āA 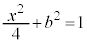 �@��
�@�� 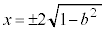
����āA�����`��x���ɕ��s��1�ӂ̒�����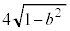 �ł��B���x���ɐ�����1�ӂ̒�����
�ł��B���x���ɐ�����1�ӂ̒�����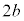 �ł��B����2�ӂ̒�������������ΐ����`�ɂȂ�̂ŁA
�ł��B����2�ӂ̒�������������ΐ����`�ɂȂ�̂ŁA ���̂Ƃ��A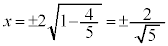
�D��萳���`�̕ӂ����ƕ��s�ɂȂ�Ȃ��ꍇ�͑��݂����A�����`��4���_�́A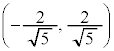 �C
�C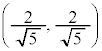 �C
�C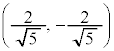 �C
�C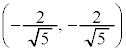 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 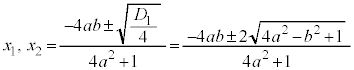 �@(�����́{��
�@(�����́{��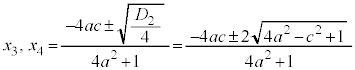 �@(�����́{��
�@(�����́{��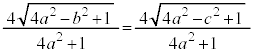
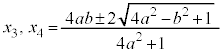 �@(�����́{��
�@(�����́{��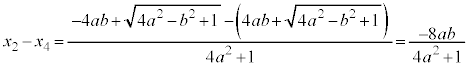
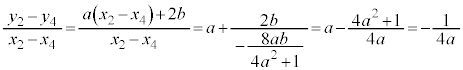
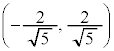 �C
�C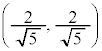 �C
�C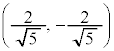 �C
�C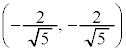 ......[��]
......[��]