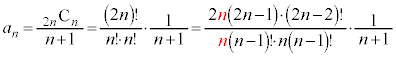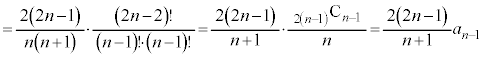���H�吔�w'21�N�O��[3]
�ȉ��̖₢�ɓ�����B
(1) ���̐���n�ɑ��āA�W���Ɋւ��鎟�̓����������B
�܂��A�����p����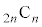 ��
��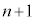 �̔{���ł��邱�Ƃ������B
�̔{���ł��邱�Ƃ������B (2) ���̐���n�ɑ��āA
�Ƃ����B���̂Ƃ��A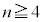 �Ȃ��
�Ȃ��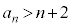 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B (3) 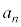 ���f���ƂȂ鐳�̐���n�����ׂċ��߂�B
���f���ƂȂ鐳�̐���n�����ׂċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�C(2)�͖��Ȃ��Ǝv���܂����A(3)�����J�ł��B�����ł͘r�s���ōs���Ă݂܂��B
����āA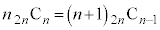 �@����@n��
�@����@n��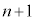 ��2�ȏ������m�����Ƃ��܂��Bp�Cq��
��2�ȏ������m�����Ƃ��܂��Bp�Cq��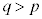 �ƂȂ鎩�R���Ƃ��āA
�ƂȂ鎩�R���Ƃ��āA 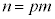 �C
�C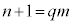
�Ƃ����܂��B�ӁX�����ƁA
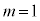 �Ɍ����A
�Ɍ����A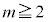 �ɔ�����̂ŁAn��
�ɔ�����̂ŁAn��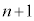 �݂͌��ɑf�ł�(�ؖ��̋Z�I���Q��)�B
�݂͌��ɑf�ł�(�ؖ��̋Z�I���Q��)�B
���̎����Ƈ@�ɂ��A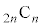 ��
��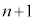 �̔{���ł��B
�̔{���ł��B(2) 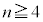 �̂Ƃ��A
�̂Ƃ��A ����āA�����܂����B
(3) 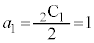 �C
�C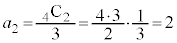 �C
�C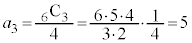 �C
�C
�Ƃ���Ă����ƁA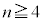 �ł́A2�ȏ�̐����̐ς̌`�ɂȂ��Ă��܂��̂ŁA�f���ɂȂ肻�����Ȃ��A�Ƃ������Ƃ��킩��܂��B
�ł́A2�ȏ�̐����̐ς̌`�ɂȂ��Ă��܂��̂ŁA�f���ɂȂ肻�����Ȃ��A�Ƃ������Ƃ��킩��܂��B
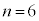 �܂Ō��Ă����ƁA
�܂Ō��Ă����ƁA ���A�����Ɗ�̐ςɂȂ肻���Ȃ̂ł����A
���A�����Ɗ�̐ςɂȂ肻���Ȃ̂ł����A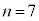 �ŁA
�ŁA �ƂȂ�j�]���܂��B�����ŁA�܂��A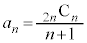 �̒��ŁA�ł��������čl���邱�Ƃɂ��܂��Bn�������̂Ƃ��ƁA��̂Ƃ��ŁA����E���q�̐��̕��ѕ��ɈႢ������̂ŁA�ꍇ�������܂��B�܂��A(1)���A
�̒��ŁA�ł��������čl���邱�Ƃɂ��܂��Bn�������̂Ƃ��ƁA��̂Ƃ��ŁA����E���q�̐��̕��ѕ��ɈႢ������̂ŁA�ꍇ�������܂��B�܂��A(1)���A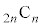 ��
��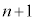 �̔{���Ȃ̂ŁA
�̔{���Ȃ̂ŁA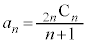 �͐����ł��B
�͐����ł��B �Ek��2�ȏ�̎��R���Ƃ��āA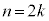 �̂Ƃ��A
�̂Ƃ��A �����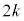 ����
����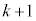 �܂ł�k�̐��ɂ��ẮA����2�{�����q�ɂ��܂��B���������
�܂ł�k�̐��ɂ��ẮA����2�{�����q�ɂ��܂��B���������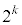 ���c��܂��B
���c��܂��B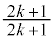 �����A�����c��́A
�����A�����c��́A 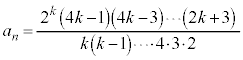 �@����B
�@����B���q��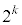 �������ƁA���ꕪ�q��
�������ƁA���ꕪ�q��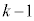 �̐��̐ςɂȂ��Ă��܂��B���q�ɕ��Ԑ��͑S��
�̐��̐ςɂȂ��Ă��܂��B���q�ɕ��Ԑ��͑S��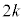 ���傫���A����ɕ��Ԑ���k�ȉ��Ȃ̂ŁA���q�ɕ��Ԋ�̒��ɑf�����������ꍇ�A����̒��ɖł��鐔�͂���܂���B
���傫���A����ɕ��Ԑ���k�ȉ��Ȃ̂ŁA���q�ɕ��Ԋ�̒��ɑf�����������ꍇ�A����̒��ɖł��鐔�͂���܂���B
�B�̕��q�̒��ɕ����̑f��������ꍇ�ɂ́A�����̑f���͕���Ɩ�邱�Ƃ͂Ȃ��̂ŁA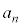 �̑f���������̒��ɕ����̑f���̐ς��o�Ă��܂��B����āA
�̑f���������̒��ɕ����̑f���̐ς��o�Ă��܂��B����āA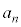 �͑f���ł͂���܂���B
�͑f���ł͂���܂���B
�B�̕��q�̒��ɑf����1�����Ȃ��ꍇ�A�����p�Ƃ���ƁA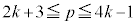 �ł����āA�B�E�ӂ̕������A
�ł����āA�B�E�ӂ̕������A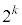 �y��
�y��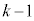 �̕����̐ςƌ��āA
�̕����̐ςƌ��āA �ƂȂ�̂ŁA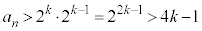 (
(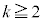 )���A
)���A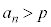
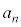 �͐����Ȃ̂ŁA����́A
�͐����Ȃ̂ŁA����́A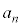 ��p��2�ȏ�̐����Ƃ̐ςɂȂ邱�Ƃ��Ӗ����A
��p��2�ȏ�̐����Ƃ̐ςɂȂ邱�Ƃ��Ӗ����A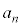 �͑f���ł͂���܂���B
�͑f���ł͂���܂���B
�B�̕��q�̒��ɑf�����Ȃ��ꍇ�́A�B�̕��q��f�����������ďo�Ă���f���̍ő�̂��̂�p�Ƃ���A�f����1�����Ȃ��ꍇ�Ɠ��l�ɁA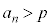 �ƂȂ�A
�ƂȂ�A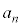 �͑f���ł͂���܂���B
�͑f���ł͂���܂���B �Ek��2�ȏ�̎��R���Ƃ��āA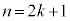 �̂Ƃ������l�ɖ���ƁA
�̂Ƃ������l�ɖ���ƁA 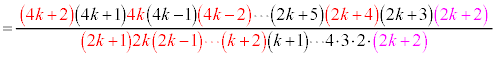
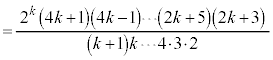 �@����C
�@����C���q��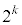 �������ƁA���ꕪ�q��k�̐��̐ςɂȂ��Ă��܂��Bn�������̏ꍇ�Ɠ��l�ɁA�C�̕��q�̒��ɑf������������A����Ɩł��Ȃ��̂ŁA
�������ƁA���ꕪ�q��k�̐��̐ςɂȂ��Ă��܂��Bn�������̏ꍇ�Ɠ��l�ɁA�C�̕��q�̒��ɑf������������A����Ɩł��Ȃ��̂ŁA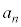 �̑f���������̒��ɂ��̂܂c��A
�̑f���������̒��ɂ��̂܂c��A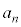 �͑f���ɂȂ�܂���B�C�̕��q�̒��ɑf����1�A���邢�͑f�����Ȃ��ꍇ�A���̑f�����A���q��f�������������Ƃ��Ɍ����ő�̑f����p�Ƃ��āA
�͑f���ɂȂ�܂���B�C�̕��q�̒��ɑf����1�A���邢�͑f�����Ȃ��ꍇ�A���̑f�����A���q��f�������������Ƃ��Ɍ����ő�̑f����p�Ƃ��āA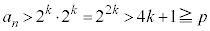 (
(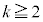 )�ƂȂ�̂ŁA
)�ƂȂ�̂ŁA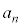 �͑f���ł͂���܂���B
�͑f���ł͂���܂���B �ȏ���A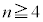 �̂Ƃ��A
�̂Ƃ��A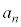 �͑f���ɂȂ�܂���B
�͑f���ɂȂ�܂���B
�A���A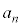 ���f���ƂȂ鐳�̐����́A
���f���ƂȂ鐳�̐����́A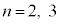 ......[��]
......[��] �ʉ��D�Q�����𗘗p���āA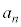 ����2�ȏ�̐����̐ς̌`�ɕ\���A�ƌ������j�ł��ł��܂��B
����2�ȏ�̐����̐ς̌`�ɕ\���A�ƌ������j�ł��ł��܂��B n��5�ȏ�̐����Ƃ��āA
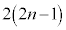 ��
��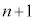 �̍ő����k�C
�̍ő����k�C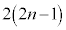 ��
��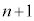 ���݂��ɑf�Ȃ�
���݂��ɑf�Ȃ�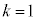 �Ƃ��܂��Bp�Cq���݂��ɑf�Ȏ��R���Ƃ��āA
�Ƃ��܂��Bp�Cq���݂��ɑf�Ȏ��R���Ƃ��āA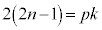 �C
�C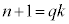 �@����D
�@����D�Ƃ����܂��B������A
(1)���A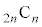 ��
��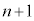 �̔{���Ȃ̂ŁA
�̔{���Ȃ̂ŁA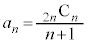 �͐����ł��B���l��
�͐����ł��B���l��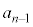 �������ł����A
�������ł����A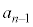 ��q�Ŋ����܂��B�����Ȃ����
��q�Ŋ����܂��B�����Ȃ����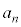 �͐����ɂȂ�Ȃ�����ł��B
�͐����ɂȂ�Ȃ�����ł��B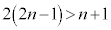 �Ȃ̂�
�Ȃ̂�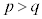 ���
���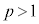 �ł��B�܂��A(2)���A
�ł��B�܂��A(2)���A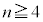 �ɂ�����
�ɂ�����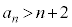 �C
�C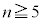 �ɂ�����
�ɂ�����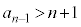 �C�D���A
�C�D���A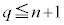 �C����āA
�C����āA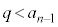 �ƂȂ�
�ƂȂ�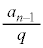 ��1���傫�Ȑ����ł��B
��1���傫�Ȑ����ł��B
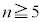 �ɂ����āA
�ɂ����āA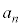 ���A1���傫��2�̐���p�C
���A1���傫��2�̐���p�C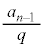 �̐ς̌`�ɂ�����̂ŁA
�̐ς̌`�ɂ�����̂ŁA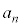 �͑f���ɂȂ�܂���B
�͑f���ɂȂ�܂���B
����āA�A���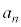 ���f���ƂȂ鐳�̐����́A
���f���ƂȂ鐳�̐����́A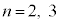
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
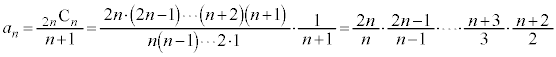
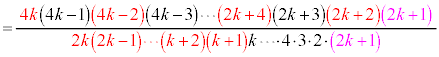
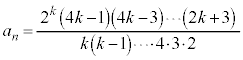 �@����B
�@����B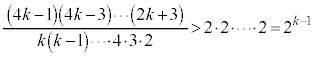
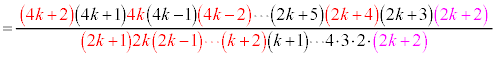
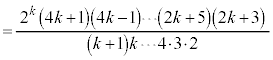 �@����C
�@����C