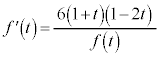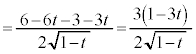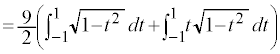東大理系数学'20年前期[3]
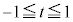 を満たす実数tに対して
を満たす実数tに対して
とする。座標平面上の点P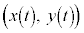 を考える。
を考える。
(1) 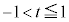 におけるtの関数
におけるtの関数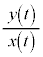 は単調に減少することを示せ。
は単調に減少することを示せ。 (2) 原点とPの距離を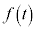 とする。
とする。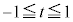 におけるtの関数
におけるtの関数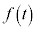 の増減を調べ、最大値を求めよ。
の増減を調べ、最大値を求めよ。 (3) t が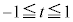 を動くときのPの軌跡をCとし、Cとx軸で囲まれた領域をDとする。原点を中心としてDを時計回りに
を動くときのPの軌跡をCとし、Cとx軸で囲まれた領域をDとする。原点を中心としてDを時計回りに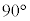 回転させるとき、Dが通過する領域の面積を求めよ。
回転させるとき、Dが通過する領域の面積を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 原点をOとして、(1)の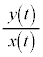 は直線OPの傾きです。t が
は直線OPの傾きです。t が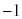 から1まで変化するとき、直線OPの傾きが単調に減少する、ということは、直線OPは時計回りに回るだけ(逆回りには動かない)、と言っています。
から1まで変化するとき、直線OPの傾きが単調に減少する、ということは、直線OPは時計回りに回るだけ(逆回りには動かない)、と言っています。
実は、ここで困ることがあります。問題文では、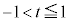 となっているのに、
となっているのに、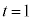 において導関数
において導関数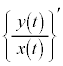 が定義できないのです。範囲を
が定義できないのです。範囲を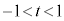 としてくれていればよいのに、出題者が少し意地悪をしています。
としてくれていればよいのに、出題者が少し意地悪をしています。
そこで、答案を書くときには、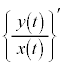 を使わずに、以下のように、違う視点から書く必要があります。
を使わずに、以下のように、違う視点から書く必要があります。 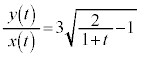 と書くと、
と書くと、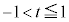 の範囲で
の範囲で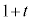 は単調に増加するので、
は単調に増加するので、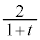 は単調に減少し、
は単調に減少し、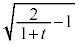 も単調に減少し、
も単調に減少し、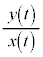 は単調に減少します。
は単調に減少します。
(2) 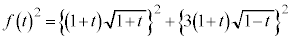
∴ 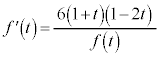
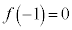 ,
,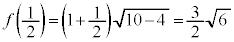 ,
,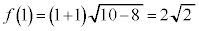 ,また、
,また、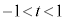 において
において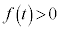 なので、
なので、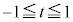 における増減表は以下(関数の増減を参照)。増減表より、
における増減表は以下(関数の増減を参照)。増減表より、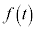 の最大値は、
の最大値は、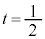 のとき、
のとき、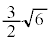 ......[答]このとき、
......[答]このとき、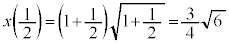 ,
,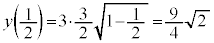 です。
です。
(3) グラフの概形を確認しておきます。
増減表は、以下のようになります。 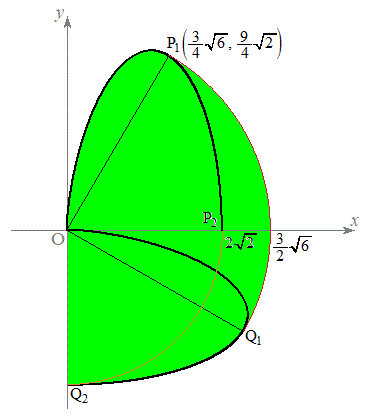 (1),(2)も考慮して、Cの概形は右図
(1),(2)も考慮して、Cの概形は右図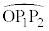 のようになります(媒介変数表示された関数のグラフを参照)。
のようになります(媒介変数表示された関数のグラフを参照)。
これを時計回りに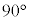 回転すると、Dの通過部分は、右図黄緑色着色部のようになります。C上で原点から最も遠い点
回転すると、Dの通過部分は、右図黄緑色着色部のようになります。C上で原点から最も遠い点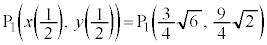 は、半径
は、半径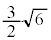 の円弧の
の円弧の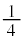 を描いて、図の点
を描いて、図の点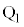 に来ます。曲線Cの端点
に来ます。曲線Cの端点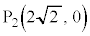 は図の点
は図の点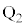 に来ます。黄緑色着色部のうち、線分
に来ます。黄緑色着色部のうち、線分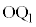 ,弧
,弧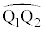 ,y軸で囲まれた部分は、線分
,y軸で囲まれた部分は、線分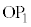 ,弧
,弧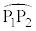 ,x軸に囲まれた部分と重なります。従って、求める面積Sは、曲線Cとx軸で囲む面積と半径
,x軸に囲まれた部分と重なります。従って、求める面積Sは、曲線Cとx軸で囲む面積と半径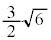 の円の面積の
の円の面積の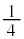 を合わせたものになります。よって、
を合わせたものになります。よって、 ここで、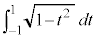 は半径1の円の面積の
は半径1の円の面積の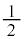 に等しく
に等しく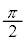 ,
,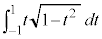 は、被積分関数
は、被積分関数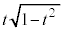 が奇関数で0,よって、
が奇関数で0,よって、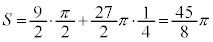 .......[答]
.......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 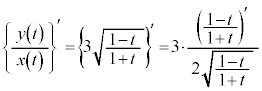
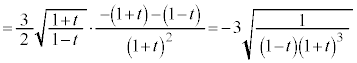
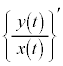 が定義できないのです。範囲を
が定義できないのです。範囲を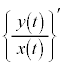 を使わずに、以下のように、違う視点から書く必要があります。
を使わずに、以下のように、違う視点から書く必要があります。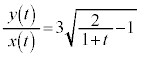 と書くと、
と書くと、