���嗝�H���w'20�N[5]
�ȉ��̖�ɓ�����B
(1) ��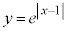 �̃O���t�Ɗ�
�̃O���t�Ɗ�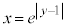 �̃O���t����̍��W���ʏ�ɕ`���B
�̃O���t����̍��W���ʏ�ɕ`���B (2) �A���s����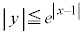 �C
�C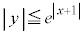 �C
�C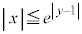 �C
�C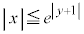 �̕\���̈��D�Ƃ���B���̂Ƃ��AD��}������B
�̕\���̈��D�Ƃ���B���̂Ƃ��AD��}������B (3) �̈�D�̖ʐς����߂�B
(4) �̈�D��x���̂܂���1��]���Ăł����]�̂̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(3)(4)�͏o��~�X�ʼns�\�A�Ƃ̂��Ƃł��B
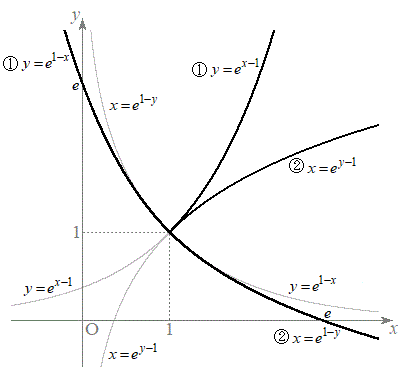
(1) 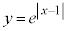 �@����@�@�̃O���t�́A
�@����@�@�̃O���t�́A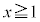 �ł�
�ł�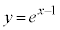 �C
�C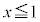 �ł�
�ł�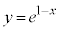 �@(�w�������Q��)
�@(�w�������Q��) 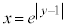 �@����A�@�̃O���t�́A
�@����A�@�̃O���t�́A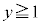 �ł�
�ł�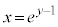 (
(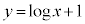 )�C
)�C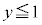 �ł�
�ł�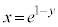 (
(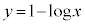 )�������܂Ƃ߂Đ}������ƁA�E�}���������B
)�������܂Ƃ߂Đ}������ƁA�E�}���������B
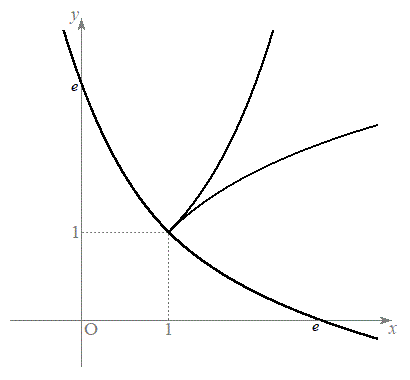
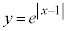 �̃O���t��
�̃O���t��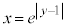 �̃O���t���o���ƁA�E�}�����B
�̃O���t���o���ƁA�E�}�����B
(2) 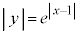 �@����B�@�̃O���t�́A
�@����B�@�̃O���t�́A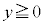 �ł͇@��
�ł͇@��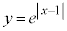 �C
�C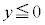 �ł�
�ł�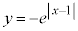 (�@��
(�@��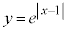 �̃O���t��x���Ɋւ��đΏ̈ړ�����������)
�̃O���t��x���Ɋւ��đΏ̈ړ�����������) 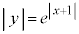 �̃O���t�́A�B��
�̃O���t�́A�B��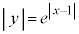 �̃O���t��x����������
�̃O���t��x����������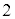 �������s�ړ��������̂ł��B
�������s�ړ��������̂ł��B
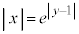 �@����C�@�̃O���t�́A
�@����C�@�̃O���t�́A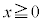 �ł͇A��
�ł͇A��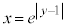 �C
�C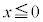 �ł�
�ł�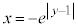 (�A��
(�A��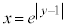 �̃O���t��y���Ɋւ��đΏ̈ړ�����������)
�̃O���t��y���Ɋւ��đΏ̈ړ�����������)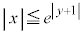 �̃O���t�́A�C��
�̃O���t�́A�C��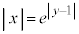 �̃O���t��y����������2�������s�ړ��������̂ł��B
�̃O���t��y����������2�������s�ړ��������̂ł��B
 �E�A���s����
�E�A���s����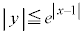 �C
�C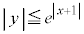 �@����D�@�̌����̈�́A
�@����D�@�̌����̈�́A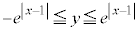 ����
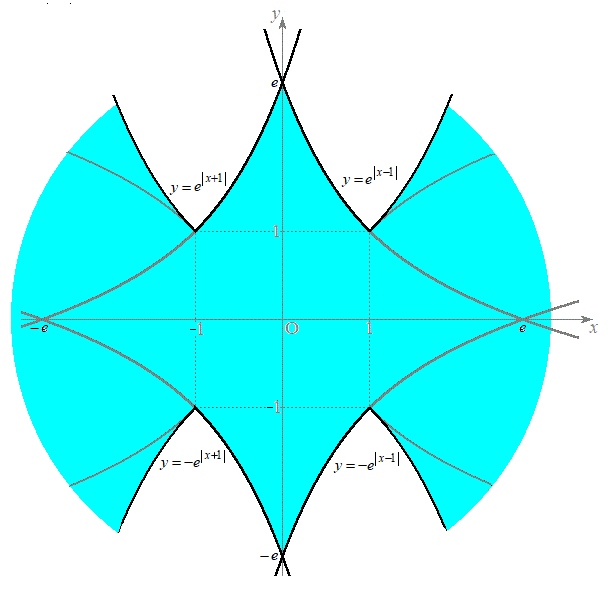
����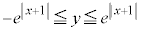 �ƂȂ��̈��ŁA�}������ƁA�E�}���F���F���B
�ƂȂ��̈��ŁA�}������ƁA�E�}���F���F���B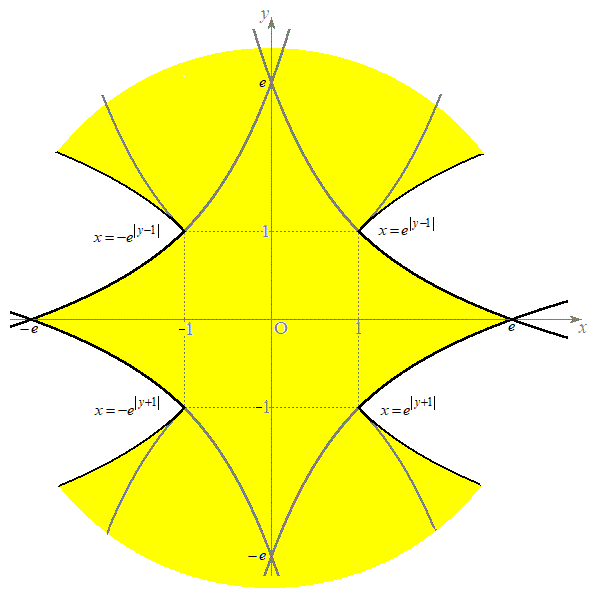 �E�A���s����
�E�A���s����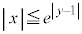 �C
�C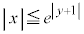 �@����E�@�̕\���̈�́A
�@����E�@�̕\���̈�́A
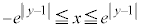 ����
����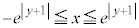 �ƂȂ�̈�ŁA�}������ƁA�E�}���F���F���B
�ƂȂ�̈�ŁA�}������ƁA�E�}���F���F���B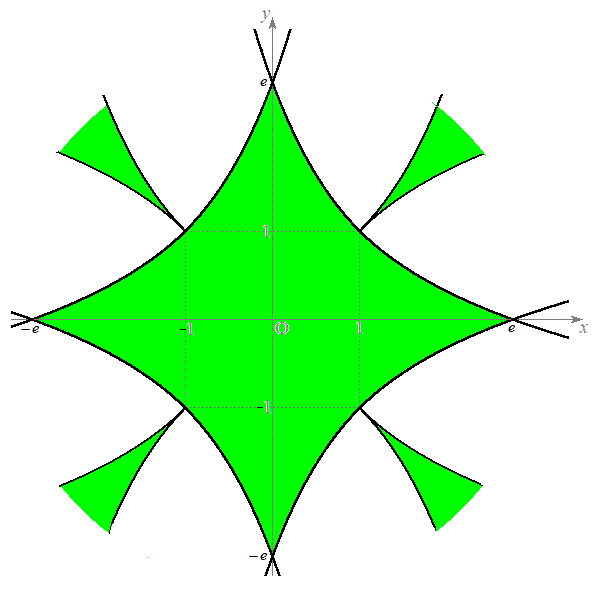 �D���E�̗̈�D�́A�D�̗̈�ƇE�̗̈�̏d�Ȃ��Ă��镔���ŁA�}������ƁA�E�}���ΐF���F��(���E���܂�)�B
�D���E�̗̈�D�́A�D�̗̈�ƇE�̗̈�̏d�Ȃ��Ă��镔���ŁA�}������ƁA�E�}���ΐF���F��(���E���܂�)�B
 (3)(4) ��蕶�̂܂܂��ƁA������Ɖ��邩�A���Ȃ��A�Ƃ��邩�ł����AD��\���A���s�������A
(3)(4) ��蕶�̂܂܂��ƁA������Ɖ��邩�A���Ȃ��A�Ƃ��邩�ł����AD��\���A���s�������A
�������Ƃ��čl���Ă݂܂��B
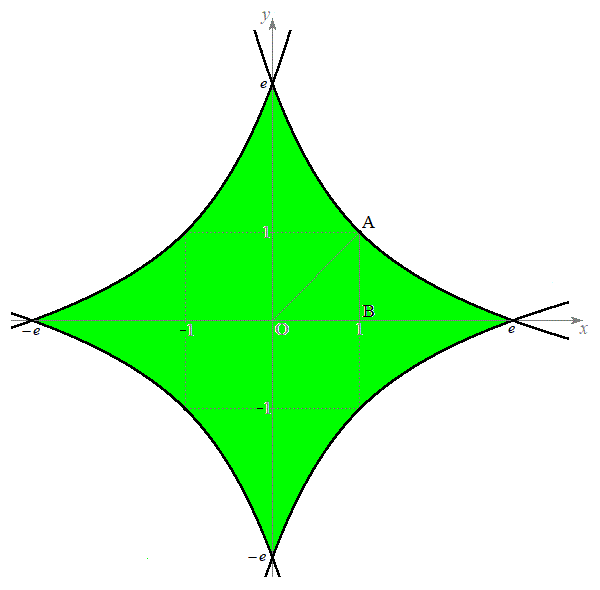
���A���̂Ƃ��̗̈�D�́A�E�}���ΐF���F��(���E���܂�)�ɂȂ�܂��B
���̂Ƃ��̗̈�D�̑�1�ی��̕����̋��E���́A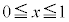 �ɂ�����
�ɂ�����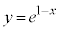 �C
�C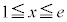 �ɂ�����
�ɂ�����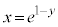 (
(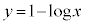 )�̈�D�̑�1�ی��̕������ʐ��́A����
)�̈�D�̑�1�ی��̕������ʐ��́A����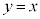 �Ɋւ���Ώ̐����A�Ȑ�
�Ɋւ���Ώ̐����A�Ȑ�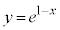 ��x���ɋ��܂ꂽ�����̂�����
��x���ɋ��܂ꂽ�����̂�����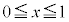 �̕����̖ʐς���A�}�́�OAB�̖ʐς�������2�{�������̂ŁA
�̕����̖ʐς���A�}�́�OAB�̖ʐς�������2�{�������̂ŁA ���߂�ʐς͂���4�{�ŁA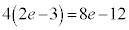 ......[��]�̈�D��x���̂܂���1��]���Ăł�����]�̂̑̐��́Ay���Ɋւ���Ώ̐����A
......[��]�̈�D��x���̂܂���1��]���Ăł�����]�̂̑̐��́Ay���Ɋւ���Ώ̐����A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 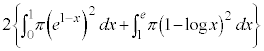
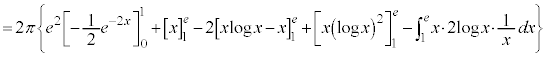
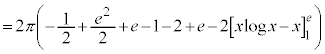
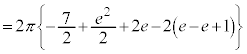
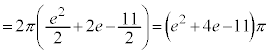 ......[��]
......[��]