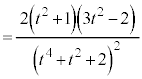早大理工数学'21年[1]
xy平面上の曲線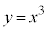 をCとする。C上の2点A
をCとする。C上の2点A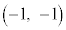 ,B
,B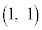 をとる。さらに、C上で原点OとBの間に動点P
をとる。さらに、C上で原点OとBの間に動点P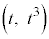 (
(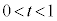 )をとる。このとき、以下の問に答えよ。
)をとる。このとき、以下の問に答えよ。
(1) 直線APとx軸のなす角をαとし、直線PBとx軸のなす角をβとするとき、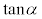 ,
,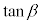 をtを用いて表せ。ただし、
をtを用いて表せ。ただし、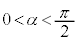 ,
,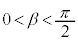 とする。
とする。 (2) 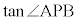 をtを用いて表せ。
をtを用いて表せ。 (3) 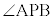 を最小にするtの値を求めよ。
を最小にするtの値を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 微分の計算問題ですが、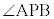 がどの角なのか注意しましょう。
がどの角なのか注意しましょう。
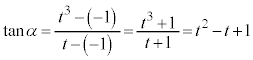 ......[答]
......[答]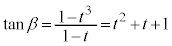 ......[答]
......[答]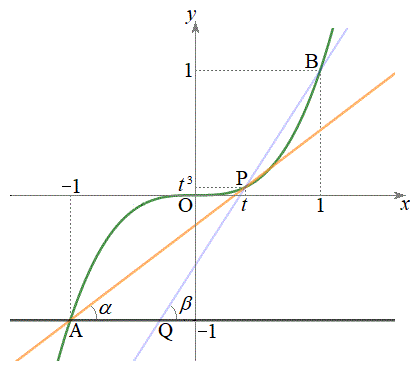 (2) まず、
(2) まず、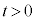 なので
なので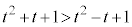 ,つまり、
,つまり、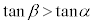 ,
,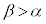 であることに注意します。点Aを通りx軸と平行な直線と直線PBとの交点をQとすると、
であることに注意します。点Aを通りx軸と平行な直線と直線PBとの交点をQとすると、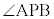 は、△APQの内角
は、△APQの内角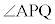 の外角で、
の外角で、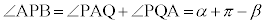 ,正接は周期πの周期関数なので、
,正接は周期πの周期関数なので、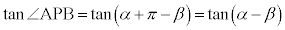
ここで、点Qのx座標は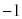 よりも大きいので、直線PBの傾きは直線ABの傾き1よりも大きく、BにおけるCの接線の傾き3 (
よりも大きいので、直線PBの傾きは直線ABの傾き1よりも大きく、BにおけるCの接線の傾き3 (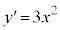 ,
,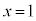 のとき
のとき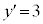 )よりも小さくなります。つまり、
)よりも小さくなります。つまり、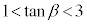
曲線Cは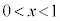 において下に凸(
において下に凸(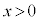 において、
において、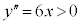 )なので、直線APの傾きは直線ABの傾き1よりも小さく、
)なので、直線APの傾きは直線ABの傾き1よりも小さく、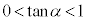
よって、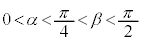 となり、
となり、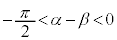 ,つまり、
,つまり、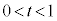 において、
において、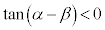 です。
です。 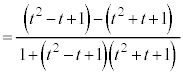
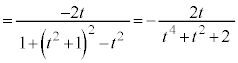 ......[答]
......[答](3) 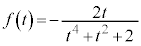 (
(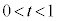 )とおき、微分すると、
)とおき、微分すると、 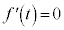 とすると、
とすると、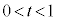 においては、
においては、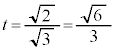
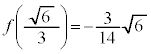 増減表は、
増減表は、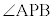 が最小のとき
が最小のとき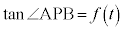 も最小で、増減表より、
も最小で、増減表より、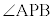 を最小にするtは、
を最小にするtは、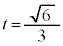 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 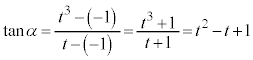 ......[答]
......[答]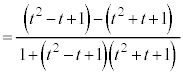
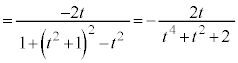 ......[答]
......[答]