���嗝�H���w'21�N[2]
����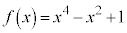 �ɂ��āA�ȉ��̖�ɓ�����B
�ɂ��āA�ȉ��̖�ɓ�����B
(1) 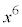 ��
��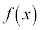 �Ŋ������Ƃ��̗]������߂�B
�Ŋ������Ƃ��̗]������߂�B (2) 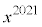 ��
��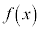 �Ŋ������Ƃ��̗]������߂�B
�Ŋ������Ƃ��̗]������߂�B (3) ���R��n��3�̔{���ł���Ƃ��A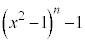 ��
��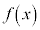 �Ŋ����邱�Ƃ������B
�Ŋ����邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@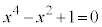 ���Ƃ���ƁA
���Ƃ���ƁA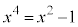 �ƂȂ�܂����A
�ƂȂ�܂����A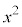 ��������
��������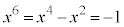 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA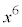 ��
��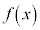 ���������]����
���������]����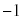 �C
�C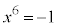 �Ȃ̂ŁA
�Ȃ̂ŁA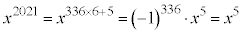 ���
���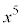 ��
��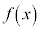 �Ŋ����ė]���
�Ŋ����ė]���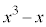 �C
�C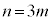 (m�͎��R��)�Ƃ����āA
(m�͎��R��)�Ƃ����āA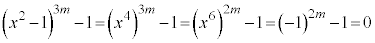 ���A
���A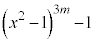 ��
�� �Ŋ�����A�Ƃ������ƂȂ̂ł����A�����ł́A�����藝��p���ĉ������Ă݂܂��B
�Ŋ�����A�Ƃ������ƂȂ̂ł����A�����ł́A�����藝��p���ĉ������Ă݂܂��B
(1) 4��������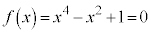 ��4����
��4����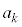 (
(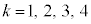 )�Ƃ��܂��B
)�Ƃ��܂��B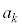 �́A
�́A �����܂��B������A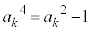 �����藧���܂��B
�����藧���܂��B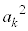 �������āA
�������āA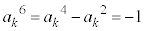 �@����@�C�܂�A
�@����@�C�܂�A �����ŁA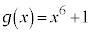 �Ƃ���ƁA
�Ƃ���ƁA ����āA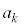 (
(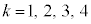 )�́A
)�́A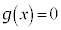 �̉��ŁA
�̉��ŁA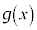 ��
��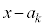 (
(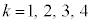 )�Ŋ����܂��B�܂�A�����藝���A
)�Ŋ����܂��B�܂�A�����藝���A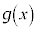 ��
��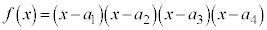 �Ŋ����܂��B����āA
�Ŋ����܂��B����āA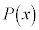 �𐮎��Ƃ��āA
�𐮎��Ƃ��āA 4����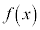 �Ŋ������]���3���ȉ����������ŁA
�Ŋ������]���3���ȉ����������ŁA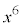 ��
��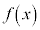 �Ŋ������Ƃ��̗]���
�Ŋ������Ƃ��̗]���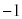 ......[��]���D
......[��]���D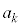 �́A
�́A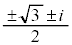 (�����C��)�ł��B[�ʉ�]�@
(�����C��)�ł��B[�ʉ�]�@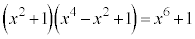 ���A
���A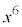 ��
��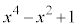 �Ŋ������]���
�Ŋ������]���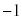 �Ƃ��邱�Ƃ��ł��܂��B�����Ȃ�����Z�����s���āA
�Ƃ��邱�Ƃ��ł��܂��B�����Ȃ�����Z�����s���āA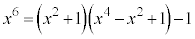 �Ƃ��ė]������߂邱�Ƃ��ł��܂��B
�Ƃ��ė]������߂邱�Ƃ��ł��܂��B (2) �@���A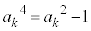 �Ȃǂ�p���āA
�Ȃǂ�p���āA 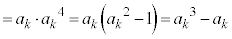 �@(
�@(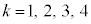 )
)�����ŁA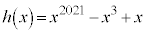 �Ƃ����ƁA
�Ƃ����ƁA ����āA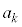 (
(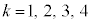 )�́A
)�́A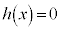 �̉��ŁA
�̉��ŁA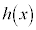 ��
��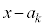 (
(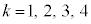 )�Ŋ����܂��B�܂�A
)�Ŋ����܂��B�܂�A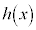 ��
��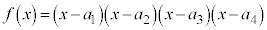 �Ŋ����܂��B����āA
�Ŋ����܂��B����āA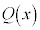 �𐮎��Ƃ��āA
�𐮎��Ƃ��āA 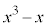 ��3���ȉ��̑������ŁA
��3���ȉ��̑������ŁA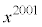 ��
��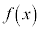 �Ŋ������Ƃ��̗]��́A
�Ŋ������Ƃ��̗]��́A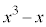 ......[��]
......[��](3) 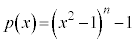 �Ƃ����ƁA
�Ƃ����ƁA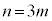 (m�͎��R��)�Ƃ��āA�@���A
(m�͎��R��)�Ƃ��āA�@���A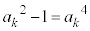 �Ȃǂ�p���āA
�Ȃǂ�p���āA 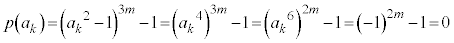 �@(
�@(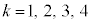 )
)����āA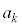 (
(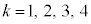 )�́A
)�́A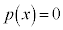 �̉��ŁA
�̉��ŁA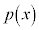 ��
��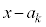 (
(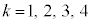 )�Ŋ����܂��B�܂�A�����藝���A
)�Ŋ����܂��B�܂�A�����藝���A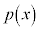 ��
��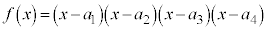 �Ŋ����܂��B
�Ŋ����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B