���嗝�H���w'21�N[3]
���f��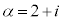 �C
�C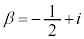 �ɑΉ����镡�f�����ʏ�̓_��
�ɑΉ����镡�f�����ʏ�̓_��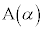 �C
�C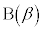 �Ƃ���B���̂Ƃ��A�ȉ��̖�ɓ�����B
�Ƃ���B���̂Ƃ��A�ȉ��̖�ɓ�����B
(1) ���f�����ʏ�̓_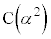 �C
�C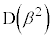 �ƌ��_O��3�_�͈꒼����ɂ��邱�Ƃ������B
�ƌ��_O��3�_�͈꒼����ɂ��邱�Ƃ������B (2) �_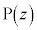 ������AB����Ƃ��A
������AB����Ƃ��A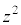 �̎�����x�C������y�Ƃ��āA�_
�̎�����x�C������y�Ƃ��āA�_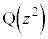 �̋O�Ղ�x�Cy�̕������ŕ\���B
�̋O�Ղ�x�Cy�̕������ŕ\���B (3) �_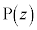 ���O�p�`OAB�̎�����ѓ����ɂ���Ƃ��A�_
���O�p�`OAB�̎�����ѓ����ɂ���Ƃ��A�_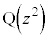 �S�̂̂Ȃ��}�`��K�Ƃ���BK�f�����ʏ�ɐ}������B
�S�̂̂Ȃ��}�`��K�Ƃ���BK�f�����ʏ�ɐ}������B (4) (3)�̐}�`K�̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@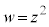 �Ƃ����ϊ��ŎO�p�`���ǂ�Ȑ}�`�Ɉڂ邩�A�Ƃ������ł��B
�Ƃ����ϊ��ŎO�p�`���ǂ�Ȑ}�`�Ɉڂ邩�A�Ƃ������ł��B
(2) 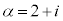 �C
�C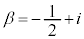 �́A�������������̂ŁA����AB��̓_
�́A�������������̂ŁA����AB��̓_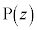 �́Ar������(
�́Ar������(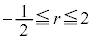 )�Ƃ��āA
)�Ƃ��āA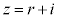 �ƕ\���܂��B
�ƕ\���܂��B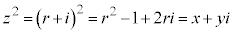 ���
��� 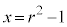 �C
�C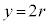 �@����@
�@����@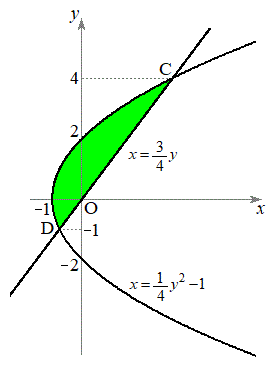 (3) ����AB��̓_�́A�@�ɂ�����
(3) ����AB��̓_�́A�@�ɂ�����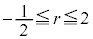 ���Az������AB��ɂ���Ƃ��A�_
���Az������AB��ɂ���Ƃ��A�_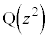 �́A�������F
�́A�������F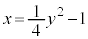 ��
��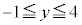 �̕����ɗ��܂��B
�̕����ɗ��܂��B����OA��̓_z�́A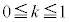 �Ƃ��āA
�Ƃ��āA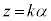 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA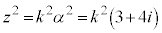 (
(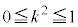 )���A�_
)���A�_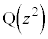 �́A���_O�Ɠ_
�́A���_O�Ɠ_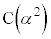 �����Ԑ����A�܂�A����
�����Ԑ����A�܂�A����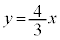 (
(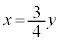 )��
)��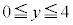 �̕����ɗ��܂��B
�̕����ɗ��܂��B
����OB��̓_z�́A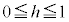 �Ƃ��āA
�Ƃ��āA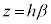 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA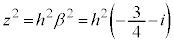 (
(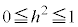 )���A�_
)���A�_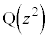 �́A���_O�Ɠ_
�́A���_O�Ɠ_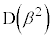 �����Ԑ����A�܂�A����
�����Ԑ����A�܂�A����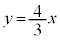 (
(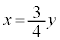 )��
)��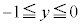 �̕����ɗ��܂��B(1)���
�̕����ɗ��܂��B(1)���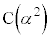 �C
�C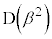 �CO�͈꒼����ɂ���̂ŁA�O�p�`OAB�̓����́A����
�CO�͈꒼����ɂ���̂ŁA�O�p�`OAB�̓����́A����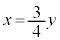 �C������
�C������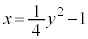 �ň͂܂ꂽ�����Ɉڂ�܂��B����āAK��}������ƁA�E�}���ΐF���F��(���E�����܂�) ......[��]
�ň͂܂ꂽ�����Ɉڂ�܂��B����āAK��}������ƁA�E�}���ΐF���F��(���E�����܂�) ......[��] ���D�O�p�`OAB�̓������A�E�}�̋��E���̓����Ɉڂ邱�Ƃɂ��ẮA����AB��̓_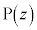 �ɂ���
�ɂ���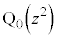 (
(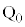 �͕�����
�͕�����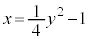 �̌�CD��̓_)�Ƃ��āA����OP��̓_
�̌�CD��̓_)�Ƃ��āA����OP��̓_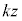 (
(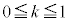 )�ɑ���
)�ɑ���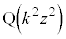 ��
��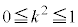 ������
������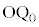 ��ɂ��邱�Ƃ��疾�炩�ł��B
��ɂ��邱�Ƃ��疾�炩�ł��B (4) K�̖ʐ�S�́A����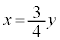 �ƕ�����
�ƕ�����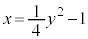 �Ƃň͂܂�镔��(K��
�Ƃň͂܂�镔��(K��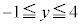 �͈̔͂ɂ���)���ʐ��ŁA
�͈̔͂ɂ���)���ʐ��ŁA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B