早大理工数学'21年[4]
n,kを2以上の自然数とする。n個の箱の中にk個の玉を無作為に入れ、各箱に入った玉の個数を数える。その最大値と最小値の差が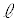 となる確率を
となる確率を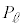 (
(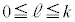 )とする。このとき、以下の問に答えよ。
)とする。このとき、以下の問に答えよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 計算は大したことはありませんが、少々思い悩むところがある問題です。n部屋にk人を入れる部屋割りの問題や、立候補者n人、投票者k人の選挙の投票パターンの問題と同じように考えます(確率を参照)。箱、玉には区別がないのですが、確率を考える場合は、区別できるものとして場合の数を数えることに注意してください。
k個の玉の1個ごとにどの箱に入るか箱の選び方がn通りあり、玉の入れ方は全部で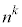 通りあり(重複順列を参照)、その各1通りは同様に確からしい。 ・・・(*)
通りあり(重複順列を参照)、その各1通りは同様に確からしい。 ・・・(*)
(1) (*)において、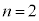 ,
,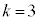 として、全事象は
として、全事象は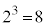 通りあります。箱を
通りあります。箱を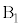 ,
,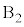 とします。
とします。 最大値と最小値の差が3になるのは、1つの箱に3個の玉が入り、もう1つの箱に玉が入らない場合で、玉が3個とも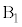 に入る場合と、3個とも
に入る場合と、3個とも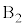 に入る場合と2通りあり、
に入る場合と2通りあり、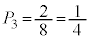 ......[答]最大値と最小値の差が2になることはなく、
......[答]最大値と最小値の差が2になることはなく、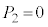 ......[答]最大値と最小値の差が1になるのは、1つの箱に2個入り、もう1つの箱に1個入る場合で、
......[答]最大値と最小値の差が1になるのは、1つの箱に2個入り、もう1つの箱に1個入る場合で、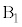 に2個、
に2個、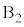 に1個入るとき、3個の玉のどれが
に1個入るとき、3個の玉のどれが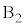 に入るかが3通りあり、
に入るかが3通りあり、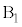 に1個、
に1個、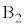 に2個入るときも3通りで、
に2個入るときも3通りで、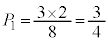 ......[答]最大値と最小値の差が0,つまり2つの箱に同数ずつ入ることはなく、
......[答]最大値と最小値の差が0,つまり2つの箱に同数ずつ入ることはなく、 ......[答]
......[答] (2) (*)において、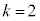 として、全事象は
として、全事象は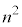 通りあります。n個の箱を
通りあります。n個の箱を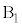 ,
,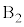 ,・・・,
,・・・,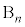 とします。
とします。 最大値と最小値の差が2になるのは、1つの箱に玉が2個入り、他の箱には玉が入らない場合です。箱を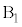 ,
,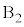 ,・・・,
,・・・,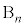 として、2個とも
として、2個とも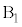 ,2個とも
,2個とも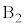 ,・・・,2個とも
,・・・,2個とも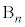 ,のn通りあり、
,のn通りあり、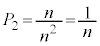 ......[答]最大値と最小値の差が1になるのは、2個の箱に玉が1個ずつ入り、他の箱に玉が入らない場合ですが、
......[答]最大値と最小値の差が1になるのは、2個の箱に玉が1個ずつ入り、他の箱に玉が入らない場合ですが、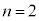 で箱が2個しかないときには、こうしたことが起こりません。従って、
で箱が2個しかないときには、こうしたことが起こりません。従って、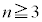 と
と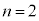 で分けて考える必要があります。
で分けて考える必要があります。
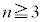 のとき、n個の箱から玉が入る2個を選ぶのが
のとき、n個の箱から玉が入る2個を選ぶのが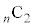 通り、仮に
通り、仮に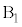 と
と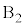 を選んだとして、2個の玉のどちらを
を選んだとして、2個の玉のどちらを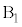 に入れるかが2通りあり、
に入れるかが2通りあり、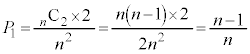 ......[答]
......[答]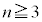 のとき、最大値と最小値の差が0,つまり、n個の箱に同数ずつ玉が入ることはなく、
のとき、最大値と最小値の差が0,つまり、n個の箱に同数ずつ玉が入ることはなく、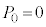 ......[答]
......[答]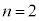 のとき、最大値と最小値の差が1になることはなく、
のとき、最大値と最小値の差が1になることはなく、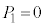 ......[答]
......[答]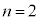 のとき、最大値と最小値の差が0になるのは、2個の箱に玉が1個ずつ入る場合で、1個の玉が
のとき、最大値と最小値の差が0になるのは、2個の箱に玉が1個ずつ入る場合で、1個の玉が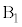 に入るか、
に入るか、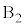 に入るか2通りあり、全事象は
に入るか2通りあり、全事象は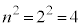 通りで、
通りで、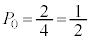 ......[答]
......[答] (3) (*)において、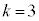 として、全事象は
として、全事象は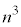 通りあります。n個の箱を
通りあります。n個の箱を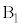 ,
,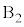 ,・・・,
,・・・,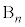 とします。
とします。 最大値と最小値の差が3になるのは、1つの箱に玉が3個入り、他の箱には玉が入らない場合です。3個とも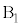 ,3個とも
,3個とも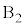 ,・・・,3個とも
,・・・,3個とも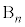 ,のn通りあり、
,のn通りあり、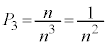 ......[答]最大値と最小値の差が2になるのは、1つの箱に2個の玉が入り、それ以外のどれか1つの箱に1個の玉が入り,他の箱には玉が入らない場合です。n個の箱から玉が入る2個を選ぶのが
......[答]最大値と最小値の差が2になるのは、1つの箱に2個の玉が入り、それ以外のどれか1つの箱に1個の玉が入り,他の箱には玉が入らない場合です。n個の箱から玉が入る2個を選ぶのが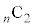 通り、仮に
通り、仮に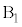 と
と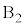 を選んだとして、2個の玉を入れるのが
を選んだとして、2個の玉を入れるのが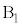 か
か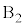 かで2通り、3個の玉のうち、1個だけ入れる箱にどの1個を入れるかが3通りあり、
かで2通り、3個の玉のうち、1個だけ入れる箱にどの1個を入れるかが3通りあり、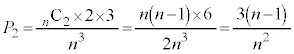 ......[答]最大値と最小値の差が1になるのは、3個の箱に玉が1個ずつ入り、他の箱に玉が入らない場合ですが、
......[答]最大値と最小値の差が1になるのは、3個の箱に玉が1個ずつ入り、他の箱に玉が入らない場合ですが、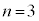 で箱が3個しかないときには、こうしたことが起こりません。従って、
で箱が3個しかないときには、こうしたことが起こりません。従って、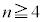 と
と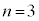 で分けて考える必要があります。
で分けて考える必要があります。
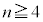 のとき、n個の箱から玉が入る3個を選び、3個の箱のどれに3個の玉のどの玉を入れるかが
のとき、n個の箱から玉が入る3個を選び、3個の箱のどれに3個の玉のどの玉を入れるかが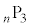 通りあり、
通りあり、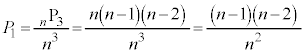 ......[答]
......[答]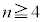 のとき、最大値と最小値の差が0,つまり、n個の箱に同数ずつ玉が入ることはなく、
のとき、最大値と最小値の差が0,つまり、n個の箱に同数ずつ玉が入ることはなく、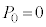 ......[答]
......[答]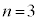 のとき、最大値と最小値の差が1になることはなく、
のとき、最大値と最小値の差が1になることはなく、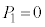 ......[答]
......[答]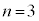 のとき、最大値と最小値の差が0になるのは、3個の箱に玉が1個ずつ入る場合で、
のとき、最大値と最小値の差が0になるのは、3個の箱に玉が1個ずつ入る場合で、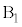 ,
,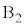 ,
,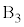 にどの玉が入るかが
にどの玉が入るかが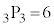 通りあり、全事象は
通りあり、全事象は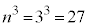 通りで、
通りで、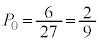 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 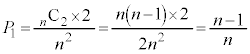 ......[答]
......[答]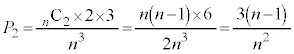 ......[答]
......[答]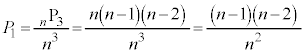 ......[答]
......[答]