���嗝�H���w'21�N[5]
���l�ʑ�OABC�ɑ��A�O�p�`ABC�̊O�S��M�Ƃ��AM�𒆐S�Ƃ��ē_A�CB�CC��ʂ鋅�ʂ�S�Ƃ���B�܂��AS�ƕ�OA�COB�COC�Ƃ̌�_�̂����AA�CB�CC�Ƃ͈قȂ���̂����ꂼ��D�CE�CF�Ƃ���B����ɁAS�ƎO�p�`OAB�̋��ʕ����Ƃ��ē������DE���l���A���̌ʂ��܂މ~���̒��S��G�Ƃ���B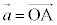 �C
�C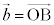 �C
�C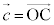 �Ƃ��āA�ȉ��̖�ɓ�����B
�Ƃ��āA�ȉ��̖�ɓ�����B
(1) 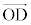 �C
�C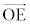 �C
�C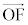 �C
�C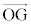 ��
��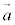 �C
�C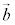 �C
�C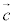 ��p���ĕ\���B
��p���ĕ\���B (2) �O�p�`OAB�̖ʐς�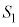 �C�l�p�`ODGE�̖ʐς�
�C�l�p�`ODGE�̖ʐς�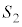 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A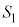 �F
�F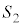 ���ł��邾���ȒP�Ȑ����ɂ��\���B
���ł��邾���ȒP�Ȑ����ɂ��\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�f���������v�Z����ƌv�Z�ʂ������Ȃ�̂ŁA�H�v���K�v�ł��B
(1) ���O�p�`�ł͊O�S�Əd�S�͈�v����(�O�p�`�̌ܐS���Q��)�̂ŁAM�͎O�p�`�̏d�S�ŁA �����ŁA���l�ʑ̂̊e�ӂ̒�����1�Ƃ���ƁAOA�COB�COC���݂̊Ԃ̂Ȃ��p��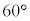 �Ȃ̂ŁA
�Ȃ̂ŁA 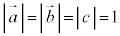 �C
�C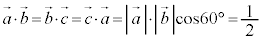 �@����A
�@����AA�CD��M�𒆐S�Ƃ��鋅��S��̓_�ŁA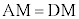 �Ƃ������Ƃ́AM�͐���AD�̐���������̓_�ŁAAD�̒��_��J�Ƃ��āAD��J����OA��̓_�ŁA
�Ƃ������Ƃ́AM�͐���AD�̐���������̓_�ŁAAD�̒��_��J�Ƃ��āAD��J����OA��̓_�ŁA �Ƃ����ƁA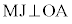 ���A
���A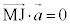 �ł��B�@���A
�ł��B�@���A 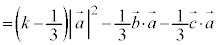
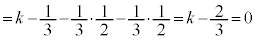 (��@�A)
(��@�A)�� 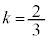 �C
�C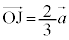
�B���A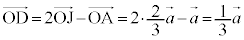 ......[��]�@����C
......[��]�@����C
���l�ʑ̂��Ώ̐����A�S�����l�ɂ��āA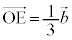 �C
�C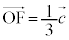 ......[��]
......[��]
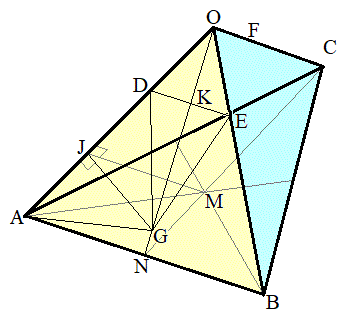 D�CE�CA�CB�͋���S��̓_�ŁA��DE���܂މ~����̓_�ł�����܂��B����āA���̉~�̒��SG�́�OAB��̓_�ŁA
D�CE�CA�CB�͋���S��̓_�ŁA��DE���܂މ~����̓_�ł�����܂��B����āA���̉~�̒��SG�́�OAB��̓_�ŁA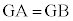 ���AG�́AAB�̐�������(O��ʂ�)��̓_�A�܂�AAB�̒��_��N�Ƃ��Ē���ON��̓_�ł��B
���AG�́AAB�̐�������(O��ʂ�)��̓_�A�܂�AAB�̒��_��N�Ƃ��Ē���ON��̓_�ł��B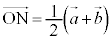 �@����D�@�Ȃ̂ŁA
�@����D�@�Ȃ̂ŁA �Ƃ����܂��B�܂��A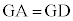 ���AG��AD�̐�������(AD�̒��_J��ʂ�OA�ɐ���)��̓_�ŁA
���AG��AD�̐�������(AD�̒��_J��ʂ�OA�ɐ���)��̓_�ŁA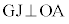 ���A
���A �� 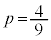 �C
�C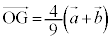 ......[��]
......[��] (2) �D��(1)��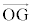 �̌��ʂ��A
�̌��ʂ��A DE��ON�̌�_��K�Ƃ��ćC���AOK�FON = OD�FOA = 1�F3 = 3�F9����āA��ODE�F��OAB = 1�F9 = 3�F27�܂��E���AOK�FKG = OK�F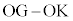 = 3�F
= 3�F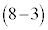 = 3�F5���A��ODE�F��DEG�F��OAB = 3�F5�F27
= 3�F5���A��ODE�F��DEG�F��OAB = 3�F5�F27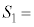 ��OAB�C�l�p�`ODGE�̖ʐ�
��OAB�C�l�p�`ODGE�̖ʐ�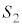 �́�ODE�{��DEG�C����āA
�́�ODE�{��DEG�C����āA 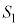 �F
�F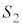 = 27�F(3+5) = 27�F8 ......[��]
= 27�F(3+5) = 27�F8 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B