���啨��'20�N�O��[2]
���̕��͂�ǂ�ŁA �ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A
�ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A �͂��ł�
�͂��ł� �ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�`��3�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������π�Ƃ���B
�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�`��3�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������π�Ƃ���B
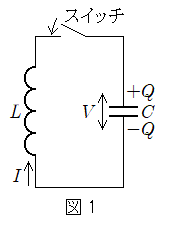
(1) �}1�̂悤�ɁA���ȃC���_�N�^���XL�̃R�C���A�X�C�b�`�A�d�C�e��C�̃R���f���T�[����Ȃ��H������B�R���f���T�[�ɒ~������d�C��Q�ƃR���f���T�[�̗��[�Ɍ����d��V�̊Ԃɂ�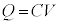 �̊W�����藧�B�R���f���T�[�ɏ����̓d�C��
�̊W�����藧�B�R���f���T�[�ɏ����̓d�C��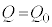 (
(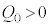 )��^���A�X�C�b�`������Ƃ���A����
)��^���A�X�C�b�`������Ƃ���A����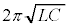 �̓d�C�U�������������B���̂Ƃ��A�}1�̃R�C���𗬂����̕����𐳂Ƃ����d��I�ɂ��āA��������
�̓d�C�U�������������B���̂Ƃ��A�}1�̃R�C���𗬂����̕����𐳂Ƃ����d��I�ɂ��āA��������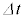 �̊Ԃ̔����ω���
�̊Ԃ̔����ω���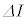 �Ƃ���ƁA�R�C���̗U���N�d�͂ƃR���f���T�[�̓d��V�̊Ԃɂ�
�Ƃ���ƁA�R�C���̗U���N�d�͂ƃR���f���T�[�̓d��V�̊Ԃɂ� 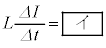 �@�@�@(i)
�@�@�@(i)�̊W������B�X�C�b�`�������A�d��I�͏����l0���畉�����ɗ���n�߂�B
�܂��A�R���f���T�[�ɒ~����ꂽ�d�C��Q�Ɠd��V�̔����ω�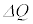 �C
�C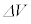 �̊ԂɁA
�̊ԂɁA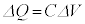 �̊W������B�d�C��Q�͓d��I�����̏ꍇ�͌������A
�̊W������B�d�C��Q�͓d��I�����̏ꍇ�͌������A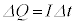 �����藧�̂ŁA��������
�����藧�̂ŁA��������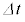 �̊Ԃ̓d��V�̔����ω�
�̊Ԃ̓d��V�̔����ω�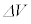 �Ɠd��I�̊Ԃɂ�
�Ɠd��I�̊Ԃɂ� 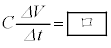 �@�@�@(ii)
�@�@�@(ii)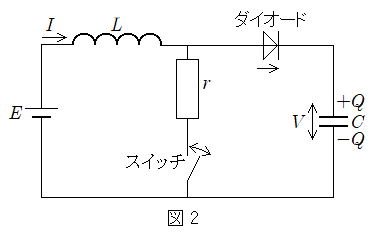
(2) �}2�̂悤�ɁA�d��E�̒����d���A���ȃC���_�N�^���XL�̃R�C���A�X�C�b�`�A��R�lr�̒�R�A�_�C�I�[�h�A�d�C�e��C�̃R���f���T�[����Ȃ��H������B�_�C�I�[�h�͗��z�I�Ȑ�����p�����Ƃ��A���Ŏ������������̒�R��0�A�t�����̒�R�͖�����Ƃ���B
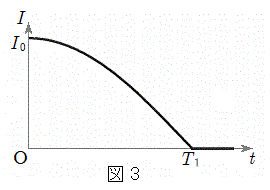
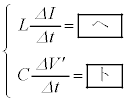 �@�@�@(iii)
�@�@�@(iii)�̊W������B��(iii)�͎�(i)�C(ii)�Ɠ����`�����Ă��邽�߁A�����l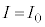 �C
�C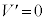 �̓d�C�U�����n�܂邪�A�_�C�I�[�h�����݂��邽�߂�I�͕��ɂȂ炸�A�}3�̂悤�Ɏ���
�̓d�C�U�����n�܂邪�A�_�C�I�[�h�����݂��邽�߂�I�͕��ɂȂ炸�A�}3�̂悤�Ɏ���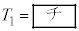 �ɐU���͒�~����B
�ɐU���͒�~����B
��1�@�R�C���ɒ~�����Ă��������̃G�l���M�[�A�d�����狟�������G�l���M�[�A�R���f���T�[�ɒ~�ς����G�l���M�[�̊W���玞��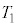 �ɂ�����R���f���T�[�̗��[�Ɍ����d�������߁AV�̎��ԕω���}3�Ɠ��l�ɕ`���B
�ɂ�����R���f���T�[�̗��[�Ɍ����d�������߁AV�̎��ԕω���}3�Ɠ��l�ɕ`���B 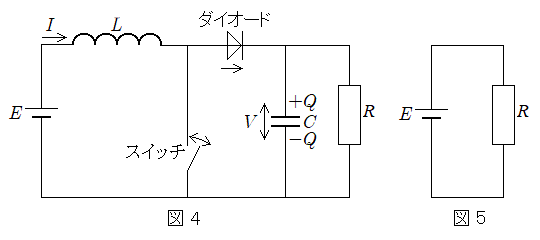
(3) �}2�̉�H�����R�lr�̒�R����苎��A��R�lR�̒�R���������}4�̉�H���A�d���ƒ�R�ڐڑ������}5�̉�H�Ɣ�r���Ă݂悤�B�������A�}4�̉�H�ł̓X�C�b�`���������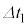 �������A���̌��������
�������A���̌��������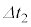 �����J���鑀����������
�����J���鑀����������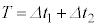 �Ŏ����I�ɂ��肩�������̂Ƃ���B�܂��A��������
�Ŏ����I�ɂ��肩�������̂Ƃ���B�܂��A��������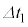 �̊Ԃ̃R�C���𗬂��d��I�C�R���f���T�[�̗��[�Ɍ����d��V�̔����ω������ꂼ��
�̊Ԃ̃R�C���𗬂��d��I�C�R���f���T�[�̗��[�Ɍ����d��V�̔����ω������ꂼ��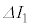 �C
�C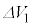 �C��������
�C��������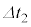 �̊Ԃ�I�CV�̔����ω������ꂼ��
�̊Ԃ�I�CV�̔����ω������ꂼ��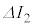 �C
�C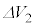 �Ƃ���B
�Ƃ���B �X�C�b�`��������Ԃł́A�d��V�𐳂Ƃ���ƃ_�C�I�[�h�ɓd���͗��ꂸ�A�d���̓d��E�ɂ��d��I�͑����A�R���f���T�[�͒�RR��ʂ��ĕ��d��
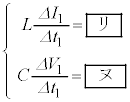 �@�@�@(iv)
�@�@�@(iv)�̊W����������B�X�C�b�`���J������Ԃł́A�d��I�𐳂Ƃ���ƃ_�C�I�[�h�ɓd��������
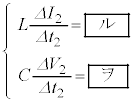 �@�@�@(v)
�@�@�@(v)�̊W����������B
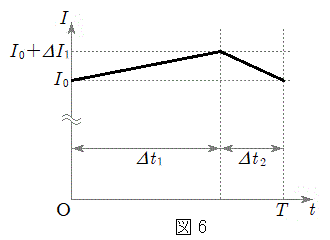 �\�����Ԃ������AI�CV����������T�Ŏ����I�ɕω��������ԂɂȂ����Ƃ���1����
�\�����Ԃ������AI�CV����������T�Ŏ����I�ɕω��������ԂɂȂ����Ƃ���1����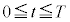 �̊Ԃ̓d��I�̕ω��͐}6�̂悤�ɂȂ����B�������A�X�C�b�`������u�Ԃ�
�̊Ԃ̓d��I�̕ω��͐}6�̂悤�ɂȂ����B�������A�X�C�b�`������u�Ԃ�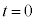 �Ƃ��A���̂Ƃ��̓d��I�Ɠd��V�����ꂼ��A
�Ƃ��A���̂Ƃ��̓d��I�Ɠd��V�����ꂼ��A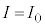 �C
�C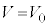 �Ƃ����B�܂��A����Ԃ�
�Ƃ����B�܂��A����Ԃ�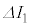 �C
�C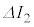 �C
�C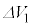 �C
�C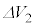 �́A��(iv)�C(v)�ɂ�����
�́A��(iv)�C(v)�ɂ�����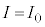 �C
�C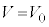 �������邱�Ƃɂ��A
�������邱�Ƃɂ��A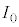 �C
�C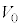 ��p���ĕ\���ł�����̂Ƃ���B
��p���ĕ\���ł�����̂Ƃ���B
��2�@����ԂɂȂ����Ƃ���1�����ł�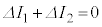 �C
�C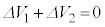 �����藧�B
�����藧�B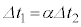 �̂Ƃ��A�d��
�̂Ƃ��A�d��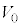 �C�d��
�C�d��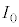 ��α�CE�CR�̂����K�v�Ȃ��̂�p���ĕ\���B�܂��A
��α�CE�CR�̂����K�v�Ȃ��̂�p���ĕ\���B�܂��A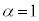 �̏ꍇ�̓d��V�̕ω����A�}6���Q�l��E�CC�CR�CT�̂����K�v�Ȃ��̂�p���ĕ`���B
�̏ꍇ�̓d��V�̕ω����A�}6���Q�l��E�CC�CR�CT�̂����K�v�Ȃ��̂�p���ĕ`���B
��3�@��2�œ���ꂽ�悤�ɁA�}4�̉�H�͓d���̓d��E�����傫�ȓd��V�����o�����Ƃ��ł���B�����Ő}4�Ɛ}5�̒�R�ŏ�����d�͂��l����B�R���f���T�[�̗��[�Ɍ����d��V�́A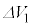 �C
�C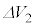 ��
��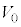 ���\���������Ƃ��A
���\���������Ƃ��A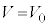 �̈��l�Ƃ݂Ȃ���B���̏ꍇ�A
�̈��l�Ƃ݂Ȃ���B���̏ꍇ�A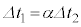 �̂Ƃ��A�}4�̒�R�ŏ�����d�͂͐}5�̒�R�ŏ�����d�͂̉��{�ɂȂ邩�Aα��p���ē�����B
�̂Ƃ��A�}4�̒�R�ŏ�����d�͂͐}5�̒�R�ŏ�����d�͂̉��{�ɂȂ邩�Aα��p���ē�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����`���b�p��H�ƌĂ����p��H�����������ł��B��蕶���Ƀq���g��������Ă���̂ŁA��蕶���悭�ǂ�ʼn��܂��傤�B
����āA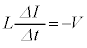 ......[��]�@(�R�C����U���N�d��
......[��]�@(�R�C����U���N�d��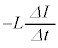 �ƍl����A
�ƍl����A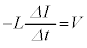 �ƂȂ�܂�)
�ƂȂ�܂�) (�n) �d�C�U���ɂ����āA(�C)�̌��ʂ��A�d��I��0���畉�����ɗ���čŏ��l�ɂȂ�Ƃ��A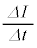 �͕��̍ŏ��l���瑝������0�ɂȂ�A�d��V�͍ő�l���猸������0�ɂȂ�܂��B����āAV��I�ɑ���
�͕��̍ŏ��l���瑝������0�ɂȂ�A�d��V�͍ő�l���猸������0�ɂȂ�܂��B����āAV��I�ɑ���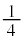 �����x��܂�(�U����1�����́A0���瑝�債�čő�l�܂ł�
�����x��܂�(�U����1�����́A0���瑝�債�čő�l�܂ł�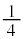 �����A�ő�l���猸������0�܂ł�
�����A�ő�l���猸������0�܂ł�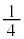 �����A0���猸�����čŏ��l�܂ł�
�����A0���猸�����čŏ��l�܂ł�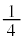 �����A�ŏ��l���瑝�債��0�܂ł�
�����A�ŏ��l���瑝�債��0�܂ł�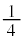 ����)�B�ʑ��̒x���
����)�B�ʑ��̒x���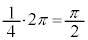 ......[��]
......[��] �}1�̐U����H�ŁA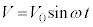 �Ƃ���ƁA
�Ƃ���ƁA �ƂȂ�̂ŁAV��I�ɑ���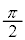 �����ʑ����x���A�ƍl���邱�Ƃ��ł��܂��B
�����ʑ����x���A�ƍl���邱�Ƃ��ł��܂��B (�j) �R�C���̓d�����ő�l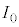 �̂Ƃ��ƁA�R���f���T�[�̓d�ׂ��ő�̂Ƃ��Ƃ̃G�l���M�[�ۑ����(�U����H���Q��)�A
�̂Ƃ��ƁA�R���f���T�[�̓d�ׂ��ő�̂Ƃ��Ƃ̃G�l���M�[�ۑ����(�U����H���Q��)�A 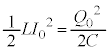 �@��
�@�� 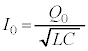 ......[��]
......[��]
(2)(�z) �\���������ԃX�C�b�`�����ƁA�R�C���̗U���N�d�͂͏��ł�(�R�C���͓����Ɠ����A�R�C���̉ߓn�������Q��)�A�_�C�I�[�h�ɂ͓d��������Ȃ��Ȃ�̂ł����A���̂Ƃ��̉�H�́A�d�rE�ɒ�Rr���ڑ�����Ă�����̂Ɠ����ł��B�R�C���ɗ����d�����I�[���̖@�����A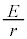 ......[��]
......[��] (�w) �X�C�b�`���J������A�d���̗����o�H�ɉ����āA�d���~���́A�R�C����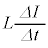 �ƃR���f���T�[���[�̓d��V�C�N�d�͂�E�C�L���q�z�b�t�̑�2�@�����A
�ƃR���f���T�[���[�̓d��V�C�N�d�͂�E�C�L���q�z�b�t�̑�2�@�����A 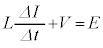 �@��
�@�� 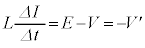 ......[��]�@(��蕶����
......[��]�@(��蕶����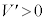 �CI�����̋L�q�ɒ���)
�CI�����̋L�q�ɒ���)(�g) E�͒萔�Ȃ̂ŁA(��)�Ɠ��l�ɁA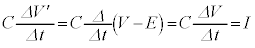 ......[��]
......[��] (�`) �}3��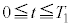 �ɂ�����I�̕ω��͓d�C�U����
�ɂ�����I�̕ω��͓d�C�U����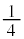 �����������Ă��܂��B����āA
�����������Ă��܂��B����āA 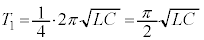 ......[��]
......[��]
��1�@�R�C���ɒ~�����Ă��������̃G�l���M�[��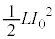 �C�X�C�b�`���J���O�ɃR���f���T�[�͓d��E�ŏ[�d����Ă����̂ŁA�R���f���T�[������
�C�X�C�b�`���J���O�ɃR���f���T�[�͓d��E�ŏ[�d����Ă����̂ŁA�R���f���T�[������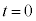 �ɒ~���Ă����d�C�ʂ�
�ɒ~���Ă����d�C�ʂ�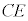 �ł��B����
�ł��B����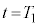 �ɂ�����R���f���T�[���[�̓d����
�ɂ�����R���f���T�[���[�̓d����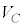 �Ƃ���ƁA���̂Ƃ��̃R���f���T�[�̓d�C�ʂ�
�Ƃ���ƁA���̂Ƃ��̃R���f���T�[�̓d�C�ʂ�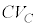 �ŁA�d�������������d�C�ʂ�
�ŁA�d�������������d�C�ʂ�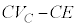 �C�d�������������G�l���M�[��
�C�d�������������G�l���M�[��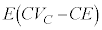 �ł��B�R���f���T�[�̎���
�ł��B�R���f���T�[�̎���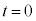 �ɂ�����Ód�G�l���M�[��
�ɂ�����Ód�G�l���M�[��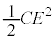 �C����
�C����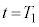 �ɂ�����Ód�G�l���M�[��
�ɂ�����Ód�G�l���M�[��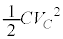 �ł��B�����̊Ԃ̃G�l���M�[�ۑ�(�U����H���Q��)���A
�ł��B�����̊Ԃ̃G�l���M�[�ۑ�(�U����H���Q��)���A �� 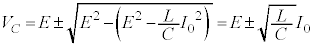
(�z)���A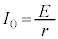 �C�܂���蕶�ɂ���ʂ�A�R���f���T�[���[�d����āA
�C�܂���蕶�ɂ���ʂ�A�R���f���T�[���[�d����āA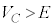 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA 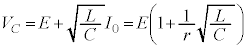 ......[��]
......[��]V�̎��ԕω��̃O���t�͉E�}�B
(3) �����ł́A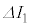 �C
�C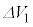 ��
��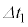 �̊Ԃ��ω����A
�̊Ԃ��ω����A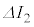 �C
�C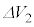 ��
��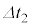 �̊Ԃ��ω����ł����āA
�̊Ԃ��ω����ł����āA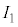 �C
�C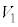 �C
�C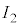 �C
�C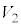 ������u�Ԃɂ�����d���A�d���̒l�A�Ɗ��Ⴂ���Ȃ��悤�ɒ��ӂ��܂��B
������u�Ԃɂ�����d���A�d���̒l�A�Ɗ��Ⴂ���Ȃ��悤�ɒ��ӂ��܂��B (��) �X�C�b�`��������Ԃ�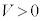 �̂Ƃ��A�_�C�I�[�h�̍��E�͕ʁX�ɓ��삵�A�L���q�z�b�t��2�@�����A
�̂Ƃ��A�_�C�I�[�h�̍��E�͕ʁX�ɓ��삵�A�L���q�z�b�t��2�@�����A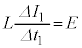 ......[��]
......[��] (�k) �I�[���̖@�����A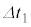 �̊Ԃ̃R���f���T�[�̓d�C�ʂ̌�����
�̊Ԃ̃R���f���T�[�̓d�C�ʂ̌�����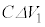 ���d��
���d��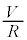 �ɂȂ�̂ŁA
�ɂȂ�̂ŁA 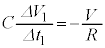 ......[��]
......[��](��) �X�C�b�`���J������ԂŁA�d���������o�H�ɉ����āA�N�d�͂�E�C�d���~���̓R�C����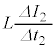 �C����ڑ����ꂽ�R���f���T�[�ƒ�R��V�C�L���q�z�b�t�̑�2�@�����A
�C����ڑ����ꂽ�R���f���T�[�ƒ�R��V�C�L���q�z�b�t�̑�2�@�����A 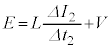 �@��
�@�� 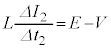 .....[��]
.....[��](��) ����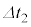 �̊ԂɁA�_�C�I�[�h��ʂ��ė��ꍞ�d��I�́A�R���f���T�[�ɗ��ꍞ��œd�C�ʂ𑝂₷����
�̊ԂɁA�_�C�I�[�h��ʂ��ė��ꍞ�d��I�́A�R���f���T�[�ɗ��ꍞ��œd�C�ʂ𑝂₷����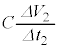 �ƒ�R�𗬂��d��
�ƒ�R�𗬂��d��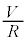 �̘a�ɂȂ�̂ŁA
�̘a�ɂȂ�̂ŁA 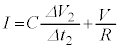 �@��
�@�� 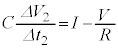 ......[��]
......[��]
��2�@��蕶���̎�(iv)(��)���A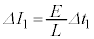 �C��(v)(��)��
�C��(v)(��)��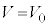 �Ƃ���(��蕶�̋L�q���A
�Ƃ���(��蕶�̋L�q���A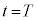 �ɂ�����V�́A
�ɂ�����V�́A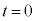 �ɂ�����
�ɂ�����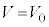 �Ɉ�v)�A
�Ɉ�v)�A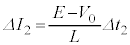 �C
�C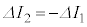 ���A
���A �� 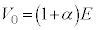 ......[��]�@����@
......[��]�@����@
��(iv)(�k)��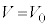 (
(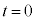 �ɂ�����
�ɂ�����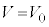 )�Ƃ��āA
)�Ƃ��āA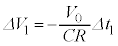 �@����A
�@����A
��(v)(��)��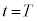 �ɂ����āA
�ɂ����āA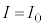 �C
�C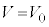 �Ƃ��āA
�Ƃ��āA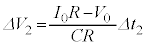
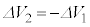 ���A
���A �@��p���āA
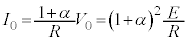 ......[��]
......[��]���D��L�ŁA����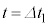 �ɂ�����d���A�d���́A
�ɂ�����d���A�d���́A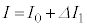 (
(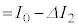 )�C
)�C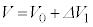 (
(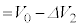 )�ł��B
)�ł��B 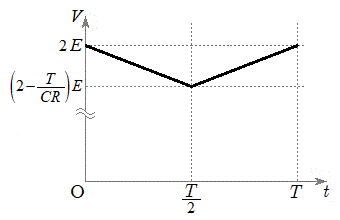
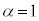 �̂Ƃ��A�@���A
�̂Ƃ��A�@���A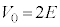 �C�A��
�C�A��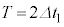 ���A
���A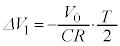 �C
�C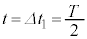 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A�d��V�̕ω��͉E�}�B
��3�@�}5�ł́A��R�ŏ������d���́A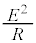 �@����B
�@����B �}4�ł́A��R�ŏ�����d�͖͂�2��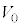 �̌��ʂ�p���āA
�̌��ʂ�p���āA 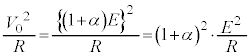 �@����C
�@����C����āA�C�͇B��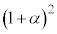 �{ ......[��]
�{ ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 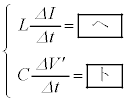 �@�@�@(iii)
�@�@�@(iii) �@�@�@(iv)
�@�@�@(iv)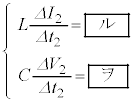 �@�@�@(v)
�@�@�@(v)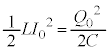 �@��
�@�� 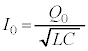 ......[��]
......[��]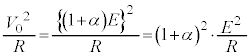 �@����C
�@����C