���啨��'20�N�O��[3]
���̕��͂�ǂ�ŁA �ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A
�ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A �͂��ł�
�͂��ł� �ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B
�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B
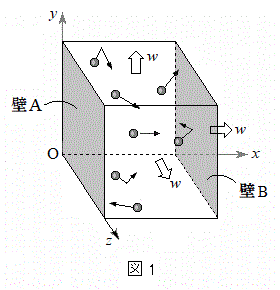
�}1�̂悤�ɁAx���Ay���Az����3�ӂƂ��闧���̂̔��̒��𑽐��̗��q(����m)���A�ǖʂɏՓ˂��Ȃ���^�����Ă���B���̗����̂̊e�ӂ̒����͈��̑���w�Ŏ��ԂƂƂ��ɑ��傷��B���Ȃ킿�A����t �ɂ�����e�ӂ̒�����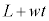 �ł���Ƃ���(L�͒萔)�B���������āA�����̂̊e�ʂ̖ʐς����ԂƂƂ��ɑ傫���Ȃ�B��̓I�ɂ́A���_O�_�Ƃ���3�̖ʂ͂��ꂼ��̈ʒu�ɌŒ肳��A����3�̖ʂ����ꂼ��ɐ����ȕ����Ɉ��̑���w�ňړ�����Ƃ���B�������A�e�ʂ��ړ����鑬��w�͗��q�̑����ɔ�ׂď\���ɏ������Ƃ���B�ȉ��ł́A
�ł���Ƃ���(L�͒萔)�B���������āA�����̂̊e�ʂ̖ʐς����ԂƂƂ��ɑ傫���Ȃ�B��̓I�ɂ́A���_O�_�Ƃ���3�̖ʂ͂��ꂼ��̈ʒu�ɌŒ肳��A����3�̖ʂ����ꂼ��ɐ����ȕ����Ɉ��̑���w�ňړ�����Ƃ���B�������A�e�ʂ��ړ����鑬��w�͗��q�̑����ɔ�ׂď\���ɏ������Ƃ���B�ȉ��ł́A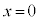 �̈ʒu�ɂ���ʂ��A�C����ɑΖʂ��Ax���̐��̌����ɑ���w�ňړ�����ʂ��B�ƌĂԁB���q�ɂ͂��炭�d�͂̉e���͖�������B
�̈ʒu�ɂ���ʂ��A�C����ɑΖʂ��Ax���̐��̌����ɑ���w�ňړ�����ʂ��B�ƌĂԁB���q�ɂ͂��炭�d�͂̉e���͖�������B
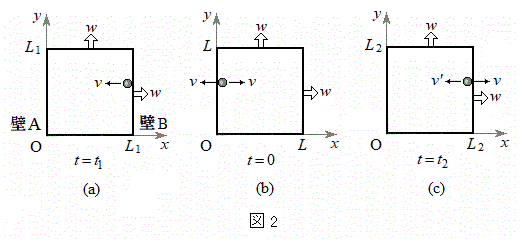 �ȉ��ł͊ȒP�̂��߂ɁA���x��x���̐����邢�͕��̕�����������1�̗��q���l���A�܂��A�}2��(a)��(b)��(c)�ŕ\���ꂽ�ߒ����l�@����B���̗��q�Ƒ��̗��q�Ƃ̏Փ˂͂Ȃ����̂Ƃ���B�}2�́A�}1�̗����̂�z���̐��̑����猩�����̂ł���B����
�ȉ��ł͊ȒP�̂��߂ɁA���x��x���̐����邢�͕��̕�����������1�̗��q���l���A�܂��A�}2��(a)��(b)��(c)�ŕ\���ꂽ�ߒ����l�@����B���̗��q�Ƒ��̗��q�Ƃ̏Փ˂͂Ȃ����̂Ƃ���B�}2�́A�}1�̗����̂�z���̐��̑����猩�����̂ł���B����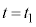 (
(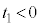 )�ɂ����āA�����̂̕ӂ̒�����
)�ɂ����āA�����̂̕ӂ̒�����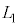 �ł���A���q�͕�B��ɂ����đ��x��x���̕��̕����������A���̑傫����v�ł���Ƃ���B���̌�A����
�ł���A���q�͕�B��ɂ����đ��x��x���̕��̕����������A���̑傫����v�ł���Ƃ���B���̌�A����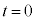 �ɂ����ė��q�͕�A�ɒe���Փ˂��A�Փˌ�̑��x��x���̐��̌����ɑ傫��v�ƂȂ����B
�ɂ����ė��q�͕�A�ɒe���Փ˂��A�Փˌ�̑��x��x���̐��̌����ɑ傫��v�ƂȂ����B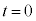 �ɂ����闧���̂̕ӂ̒�����L�ł���B����Ɏ���
�ɂ����闧���̂̕ӂ̒�����L�ł���B����Ɏ���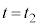 (
(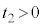 )�ɂ����āA���q�͕�B�ɒe���Փ˂��A����̑��x��x���̕��̌����ɑ傫��
)�ɂ����āA���q�͕�B�ɒe���Փ˂��A����̑��x��x���̕��̌����ɑ傫��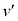 �ƂȂ����B
�ƂȂ����B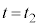 �ɂ����闧���̂̕ӂ̒�����
�ɂ����闧���̂̕ӂ̒�����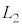 �ł������B
�ł������B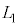 ��
��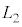 ��L�Cv�Cw��p���ĕ\����
��L�Cv�Cw��p���ĕ\���� �C
�C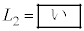 �ł���A�}2�̉ߒ��̎���
�ł���A�}2�̉ߒ��̎���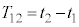 ��L�Cv�Cw��p����
��L�Cv�Cw��p����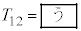 �ƕ\�����B����ɁAw��v�ɔ�ׂď\���ɏ��������߁A
�ƕ\�����B����ɁAw��v�ɔ�ׂď\���ɏ��������߁A ��L�Cv�C
��L�Cv�C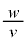 �ŕ\���A������
�ŕ\���A������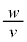 ��2���ȏ������ߎ����s���ƁA
��2���ȏ������ߎ����s���ƁA �ƂȂ�B�Ȃ��A�K�v�Ȃ炻�̐�Βl�������Ȏ���x�ɑ���ߎ���
�ƂȂ�B�Ȃ��A�K�v�Ȃ炻�̐�Βl�������Ȏ���x�ɑ���ߎ���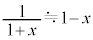 ��p���Ă悢�B��A�����q�����x�������̗͂̎��ԕ���
��p���Ă悢�B��A�����q�����x�������̗͂̎��ԕ���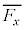 �́A���q����͐�
�́A���q����͐�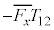 ������
������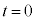 �ɂ�����Փ˂ł̗��q��x�������̉^���ʕω��ɓ������Ƃ����W�����狁�܂�B�����ŁA��A�����q����鈳��P���A
�ɂ�����Փ˂ł̗��q��x�������̉^���ʕω��ɓ������Ƃ����W�����狁�܂�B�����ŁA��A�����q����鈳��P���A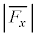 ���A�̖ʐςŊ��������̂Ƃ���B
���A�̖ʐςŊ��������̂Ƃ���B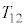 �Ƃ���
�Ƃ���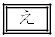 ��p���A��A�̖ʐς��Փˎ���
��p���A��A�̖ʐς��Փˎ���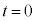 �ł�
�ł�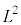 �ł���Ƃ���ƁAm�Cv�CL��p����
�ł���Ƃ���ƁAm�Cv�CL��p���� �ƂȂ�B�Ȃ��A
�ƂȂ�B�Ȃ��A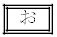 ��w�ɂ͂��Ȃ��ʂł���B
��w�ɂ͂��Ȃ��ʂł���B
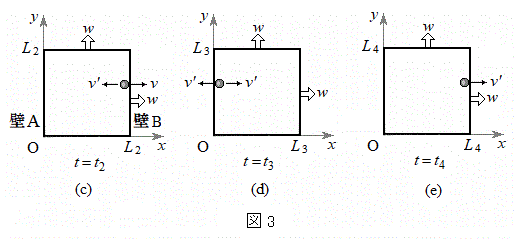 ���ɁA�}3��(c)��(d)��(e)�ŕ\�����A����
���ɁA�}3��(c)��(d)��(e)�ŕ\�����A����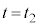 �ɑ���
�ɑ��� �ŕ�B�𗣂ꂽ���q���A�Ăѕ�A�ɒe���Փ˂��A��B�ɖ߂��Ă���܂ł̉ߒ����l����B�܂��A
�ŕ�B�𗣂ꂽ���q���A�Ăѕ�A�ɒe���Փ˂��A��B�ɖ߂��Ă���܂ł̉ߒ����l����B�܂��A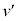 ��v��w�ɂ��
��v��w�ɂ��
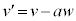 �@(i)
�@(i)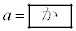 �ł���B�������A�ȉ��̉ł́A�w�肳�ꂽ�ꍇ�������A
�ł���B�������A�ȉ��̉ł́A�w�肳�ꂽ�ꍇ�������A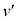 ��v��w�ŕ\���ۂ́Aa��p������(i)�̉E�ӂ̕\����p���邱�ƁB���q������
��v��w�ŕ\���ۂ́Aa��p������(i)�̉E�ӂ̕\����p���邱�ƁB���q������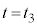 �ɕ�A�ɒe���Փ˂������̗����̂̕ӂ̒���
�ɕ�A�ɒe���Փ˂������̗����̂̕ӂ̒���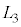 ��L�Cv�C
��L�Cv�C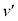 �Cw��p����
�Cw��p����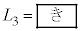 �ƂȂ�B�}3�̉ߒ��ɂ���A�����q����鈳��
�ƂȂ�B�}3�̉ߒ��ɂ���A�����q����鈳�� �́A�}2�̉ߒ��ɑ���
�́A�}2�̉ߒ��ɑ���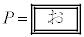 �̌��ʂɂ����āAv��
�̌��ʂɂ����āAv��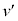 �ɁAL��
�ɁAL��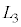 �ɒu�������邱�Ƃœ�����B�����ŁA���͂̕ω���
�ɒu�������邱�Ƃœ�����B�����ŁA���͂̕ω���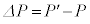 ���l���A��
���l���A��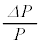 ��
��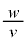 �̊��Ƃ��ĕ\���A
�̊��Ƃ��ĕ\���A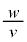 ��2���ȏ�������
��2���ȏ�������
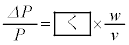 �@(ii)
�@(ii) ��a��p���ĕ\�����ʂł���B��(ii)�̓��o�ɂ����āA�K�v�Ȃ�A���̐�Βl�������Ȏ���x��2���ȏ������ߎ���
��a��p���ĕ\�����ʂł���B��(ii)�̓��o�ɂ����āA�K�v�Ȃ�A���̐�Βl�������Ȏ���x��2���ȏ������ߎ���
�ł��邱�Ƃ�p���Ă悢�B�����ŁA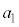 �C
�C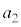 �C
�C �C
�C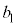 �C
�C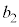 �C
�C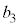 �Cc�͔C�ӂ̎����ł���B
�Cc�͔C�ӂ̎����ł���B
����ɁA�}2�̉ߒ��ł̗��q�̕�A�ւ̏Փˎ���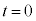 �ɂ����闧���̂̑̐�
�ɂ����闧���̂̑̐�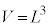 �ƁA�}3�̉ߒ��ł̏Փˎ���
�ƁA�}3�̉ߒ��ł̏Փˎ���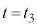 �ɂ�����̐�
�ɂ�����̐� �ɑ��āA�̐ς̕ω���
�ɑ��āA�̐ς̕ω���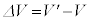 ���l����B��
���l����B��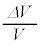 ��
��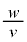 �̊��Ƃ��ĕ\���A
�̊��Ƃ��ĕ\���A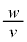 ��2���ȏ�������
��2���ȏ�������
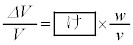 �@(iii)
�@(iii)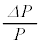 ��
�� �̊Ԃ�
�̊Ԃ�
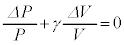 �@(iv)
�@(iv)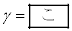 �ŗ^������B
�ŗ^������B
�ȏ�̎�(iv)�̓��o�́Ax�������ɂ̂݉^������1�̗��q�ɒ��ڂ������̂ł���A����P�͂��̗��q�݂̂����A���鈳�͂ł������B�������AP������������ɉ^������S�Ă̗��q�����A���鈳�͂Ƃ��A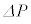 ��
��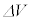 ��^����ꂽ�������ԓ��ł̕ω����Ƃ��Ă��A��(iv)�����藧���Ƃ��������B����ɁAP��
��^����ꂽ�������ԓ��ł̕ω����Ƃ��Ă��A��(iv)�����藧���Ƃ��������B����ɁAP��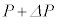 �ɁAV��
�ɁAV��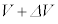 �ɔ����ɕω�����Ԃɗ����̓��̗��q����Ȃ闝�z�C�̂̐�Ή��x��T����
�ɔ����ɕω�����Ԃɗ����̓��̗��q����Ȃ闝�z�C�̂̐�Ή��x��T����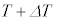 �ɔ����ɕω������Ƃ���ƁA��(iv)�͗��z�C�̂̏�ԕ�������p���邱�ƂŁA
�ɔ����ɕω������Ƃ���ƁA��(iv)�͗��z�C�̂̏�ԕ�������p���邱�ƂŁA
�ƕ\�����Ƃ��ł���B�����ŁA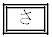 ��γ��p���ĕ\�����ʂł���A������
��γ��p���ĕ\�����ʂł���A������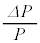 �C
�C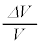 �C
�C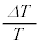 ��2���ȏ�������B
��2���ȏ�������B
�W��(iv)�́A���z�C�̂̒f�M�ω��ɂ�����|�A�\���̖@���Ƃ��Ēm��ꂽ���̂ł���Aa�̒l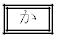 ��������γ�̒l
��������γ�̒l �͒P���q���q�C�̂̂��̂��Č����Ă���B�������A�����q���q�C�̂̏ꍇ�́A��(iv)�̒萔γ��
�͒P���q���q�C�̂̂��̂��Č����Ă���B�������A�����q���q�C�̂̏ꍇ�́A��(iv)�̒萔γ�� �Ƃ͈قȂ�l���Ƃ�B
�Ƃ͈قȂ�l���Ƃ�B
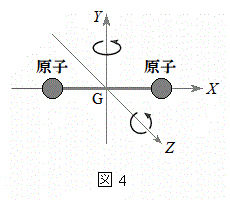 �����ŁA�}1�̗����̓���x�������ɉ^������1���q���Ăэl���A���̂悤�ȃ��f����p���āA�q���q�C�̂ɑ��鎮(iv)��γ�����߂Ă݂悤�B�q���q��2�̎��_(���q)���������Ŏ��ʂ��ł���܂������Ȗ_�łȂ��������̂ƌ��Ȃ��ƁA���̓q���q�ɂ͏d�S�̕��i�^���̑��ɁA�}4�̂悤�ɁA�d�S(�}4�̌��_G)�̂܂��́AY����Z������]���Ƃ���2�̉�]�^��������B���܁A�}1�̗����̂̒���x�������ɕ��i�^������q���q�ɑ��Đ}2�Ɛ}3�̉ߒ����l����B���̓q���q�̃G�l���M�[E�́A�d�S��x�������̕��i�^���̃G�l���M�[
�����ŁA�}1�̗����̓���x�������ɉ^������1���q���Ăэl���A���̂悤�ȃ��f����p���āA�q���q�C�̂ɑ��鎮(iv)��γ�����߂Ă݂悤�B�q���q��2�̎��_(���q)���������Ŏ��ʂ��ł���܂������Ȗ_�łȂ��������̂ƌ��Ȃ��ƁA���̓q���q�ɂ͏d�S�̕��i�^���̑��ɁA�}4�̂悤�ɁA�d�S(�}4�̌��_G)�̂܂��́AY����Z������]���Ƃ���2�̉�]�^��������B���܁A�}1�̗����̂̒���x�������ɕ��i�^������q���q�ɑ��Đ}2�Ɛ}3�̉ߒ����l����B���̓q���q�̃G�l���M�[E�́A�d�S��x�������̕��i�^���̃G�l���M�[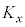 �Əd�S�̂܂���2�̉�]�^���̃G�l���M�[�̘a�ł���Ƃ��A�e��]�^���̃G�l���M�[�̒l���ǂ��
�Əd�S�̂܂���2�̉�]�^���̃G�l���M�[�̘a�ł���Ƃ��A�e��]�^���̃G�l���M�[�̒l���ǂ��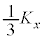 �ɓ������A
�ɓ������A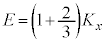 �̊W����ɐ��藧���Ă���Ɖ��肷��B���̏ꍇ�́A�}2(c)�ŕ\���ꂽ�A����
�̊W����ɐ��藧���Ă���Ɖ��肷��B���̏ꍇ�́A�}2(c)�ŕ\���ꂽ�A����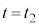 �ɂ����镪�q�ƕ�B�̏Փˌ�̕��q�̑���
�ɂ����镪�q�ƕ�B�̏Փˌ�̕��q�̑���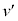 �����߂邽�߂ɁA���̏Փ˂�q���q(����m)�ƕ�B�ɑΉ������d������(����M)��x�������̏Փˉߒ��ɒu�������A�Ō�Ɏ���M������m�ɔ�ׂď\���ɑ傫������B���̏Փ˂ɂ����āA�}4�̓q���q�̍\���ڂɍl������K�v�͂Ȃ��A�q���q�͏�L�̃G�l���M�[E������������m�̗��q�ƍl����悢�B�ՓˑO��̕��q�ƕ��̂̑��x�͐}5�̒ʂ�Ƃ���B
�����߂邽�߂ɁA���̏Փ˂�q���q(����m)�ƕ�B�ɑΉ������d������(����M)��x�������̏Փˉߒ��ɒu�������A�Ō�Ɏ���M������m�ɔ�ׂď\���ɑ傫������B���̏Փ˂ɂ����āA�}4�̓q���q�̍\���ڂɍl������K�v�͂Ȃ��A�q���q�͏�L�̃G�l���M�[E������������m�̗��q�ƍl����悢�B�ՓˑO��̕��q�ƕ��̂̑��x�͐}5�̒ʂ�Ƃ���B
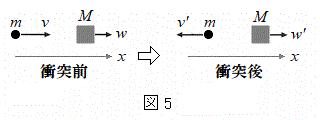
��1�@�}5�̏Փˉߒ��ɂ�����G�l���M�[�ۑ��Ɖ^���ʕۑ��̊W���������������B�������A�Փˌ�̓q���q�̑���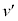 ��v�Cw�C
��v�Cw�C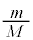 ��p���ĕ\�킹�B�Ȃ��A
��p���ĕ\�킹�B�Ȃ��A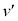 �o����r���v�Z�������K�v�͂Ȃ��B
�o����r���v�Z�������K�v�͂Ȃ��B
��2�@��1�ŋ��߂�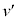 �ɂ�����M��m�ɔ�ׂď\���ɑ傫������B���Ȃ킿�A
�ɂ�����M��m�ɔ�ׂď\���ɑ傫������B���Ȃ킿�A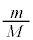 ���ߎ��I��0�Ƃ��āA�q���q�C�̂̏ꍇ�̎�(i)��a�̒l�Ǝ�(iv)��γ�̒l�����߂�B
���ߎ��I��0�Ƃ��āA�q���q�C�̂̏ꍇ�̎�(i)��a�̒l�Ǝ�(iv)��γ�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�C�̕��q�^���_�́A�ʏ�̓������ł��P���q���q���z�C���̒�ϕω����������Ƃ������̂ł����A�{��ł́A�f�M�ω��̉ߒ����l�@���ĒP���q���q�C�̂̔�M������߂邾���łȂ��A���f������蕶���̐}�Ƃ��ė^�����Ă���Ƃ͂����A�����2���q���q�̏ꍇ�̔�M��܂ŋ��߂�A�Ƃ����ߑ�ȓ��e�ɂȂ��Ă��āA���Ƃ��������łȂ��v�Z����ςŁA�ߎ��̕��@�Ȃǐe�ȗU�������Ă͂��܂����A�����͌��������ł��B
���@���q�́A����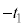 (
(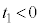 )�̊Ԃɑ���v�ŋ���
)�̊Ԃɑ���v�ŋ���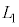 �i�ނ̂ŁA
�i�ނ̂ŁA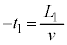 �C����A����
�C����A����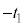 �̊Ԃɕ�B�͑���w�ŋ���
�̊Ԃɕ�B�͑���w�ŋ���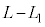 ���������̂ŁA
���������̂ŁA ���@���q�́A����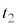 �̊Ԃɑ���v�ŋ���
�̊Ԃɑ���v�ŋ���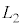 �i�ނ̂ŁA
�i�ނ̂ŁA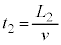 �C����A����
�C����A����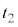 �̊Ԃɕ�B�͑���w�ŋ���
�̊Ԃɕ�B�͑���w�ŋ���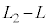 ���������̂ŁA
���������̂ŁA ���@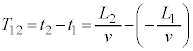
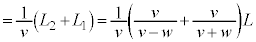
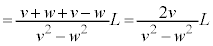 ......[��]
......[��]���@ �̌��ʂŁA����E���q��
�̌��ʂŁA����E���q�� �Ŋ����蕶�̋ߎ����s��
�Ŋ����蕶�̋ߎ����s��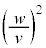 ������ƁA
������ƁA 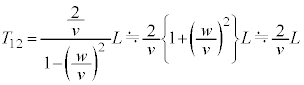 ......[��]
......[��]���@����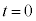 �ɂ�����Փ˂ł̗��q��x�������̉^���ʕω��́A
�ɂ�����Փ˂ł̗��q��x�������̉^���ʕω��́A  �̌��ʂ�p���āA
�̌��ʂ�p���āA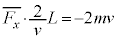 �@��
�@�� 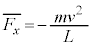
��A�̖ʐς�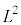 �ł��邱�Ƃ���A
�ł��邱�Ƃ���A 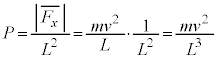 ......[��]
......[��]���@���q�́A����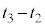 �̊Ԃɑ���
�̊Ԃɑ���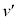 �ŋ���
�ŋ���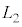 �i�ނ̂ŁA
�i�ނ̂ŁA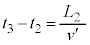 �C����A����
�C����A����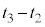 �̊Ԃɕ�B�͑���w�ŋ���
�̊Ԃɕ�B�͑���w�ŋ��� ���������̂ŁA
���������̂ŁA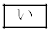 �̌��ʂ�p���āA
�̌��ʂ�p���āA �� 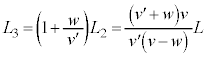 ......[��]
......[��] ��蕶�ɂ���悤�ɁAa��p���ĕ\���̂ŁA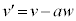 �Ƃ��邱�Ƃɒ��ӂ��܂��B�r���A
�Ƃ��邱�Ƃɒ��ӂ��܂��B�r���A �C
�C �̌��ʂ��g���āA
�̌��ʂ��g���āA ��蕶�̋ߎ�����p����(�ߎ����ɂ�����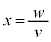 �C
�C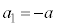 �C
�C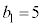 �C
�C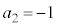 �C
�C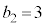 �C
�C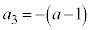 �C
�C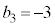 �Ƃ���)�A
�Ƃ���)�A �� 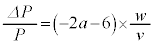 �@
�@ ......[��]
......[��] ���@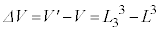 ��
�� �̌��ʂ��A
�̌��ʂ��A �����ł���蕶�̋ߎ�����p���āA
6 ......[��]
���@ �C
�C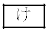 �̌��ʂ�p���āA
�̌��ʂ�p���āA �� 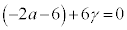 �C����āA
�C����āA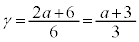 ......[��]
......[��] ���@�����̓��ɗ��q��n��������A�C�̒萔��R�Ƃ��āA���z�C�̂���ԕ������́A  �@����@
�@����@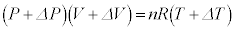 �@����A
�@����A�A�|�@�Ƃ��āA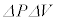 ������ƁA
������ƁA ���ӂ�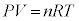 �ŕӁX����ƁA
�ŕӁX����ƁA 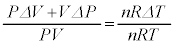 �@��
�@�� 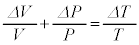
��蕶��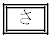 ��γ��p���ĕ\�����ʂƏ�����Ă���̂ŁA(iv)����p���āA
��γ��p���ĕ\�����ʂƏ�����Ă���̂ŁA(iv)����p���āA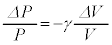 �C����āA
�C����āA �܂�A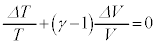 �@
�@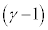 ......[��]
......[��] ���@ �̌��ʂ�
�̌��ʂ�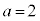 �������āA
�������āA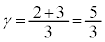 ......[��]
......[��]
��1�@�ՓˑO(����v)�̓q���q�����i�^���̃G�l���M�[��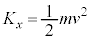 �Ȃ̂ŁA�d�S�̂܂���2�̉�]�^���̃G�l���M�[���܂߂āA�q���q�̃G�l���M�[�́A
�Ȃ̂ŁA�d�S�̂܂���2�̉�]�^���̃G�l���M�[���܂߂āA�q���q�̃G�l���M�[�́A �Փˌ�(����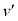 )�̓q���q�̃G�l���M�[�͓��l�ɁA
)�̓q���q�̃G�l���M�[�͓��l�ɁA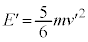
����āA�G�l���M�[�ۑ��̊W���́A 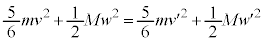 �@����B
�@����B �@����C
�@����C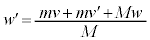
�B�ɑ�����āA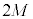 ��������ƁA
��������ƁA ��������m�Ŋ���ƁA
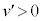 �C
�C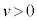 �Ȃ̂ŁA
�Ȃ̂ŁA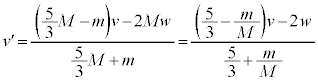 �@����D
�@����D
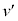 �̓��o�ߒ��͉Ƃ��ėv������Ă��Ȃ��̂ŁA�B�C�C�C�D���Ƃ��܂��B
�̓��o�ߒ��͉Ƃ��ėv������Ă��Ȃ��̂ŁA�B�C�C�C�D���Ƃ��܂��B
��2�@�D��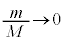 �Ƃ����(���̋Ɍ����Q��)�A
�Ƃ����(���̋Ɍ����Q��)�A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
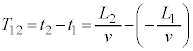
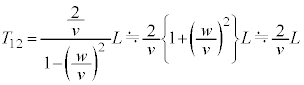 ......[��]
......[��]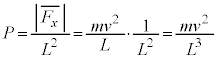 ......[��]
......[��]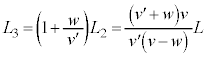 ......[��]
......[��]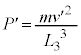
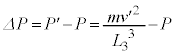
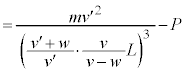
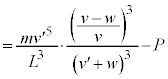
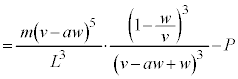
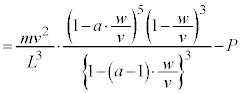
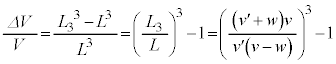
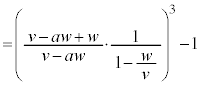

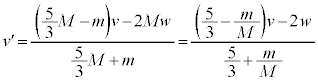 �@����D
�@����D
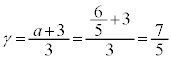 ......[��]
......[��]