微分法の方程式への応用(2) 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
例1.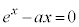 の解の個数がaの値によりどう変化をするかを調べる。
の解の個数がaの値によりどう変化をするかを調べる。
 [解法1] 方程式を、
[解法1] 方程式を、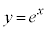 と
と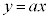 の連立方程式と見て、双方のグラフを調べます。
の連立方程式と見て、双方のグラフを調べます。
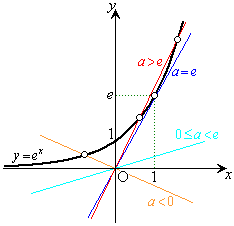
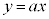 のグラフは、原点を通る傾きaの直線です。傾きaを変化させでみます。
のグラフは、原点を通る傾きaの直線です。傾きaを変化させでみます。
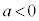 の場合には、原点を通る傾き負の直線と
の場合には、原点を通る傾き負の直線と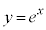 は第2象限で交わります。
は第2象限で交わります。
従って、解は1個です。
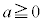 の場合には、
の場合には、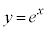 は単調増加かつグラフは下に凸なので、傾きaを大きくしていくと、aが小さいうちは曲線の下を直線が通過するのに、やがて、直線が曲線に接するようになり、さらにaを大きくすると、直線と
は単調増加かつグラフは下に凸なので、傾きaを大きくしていくと、aが小さいうちは曲線の下を直線が通過するのに、やがて、直線が曲線に接するようになり、さらにaを大きくすると、直線と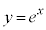 が2交点をもつようになります。
が2交点をもつようになります。
直線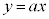 が
が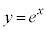 に接するときを調べます。
に接するときを調べます。
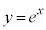 の導関数は、の導関数は、
の導関数は、の導関数は、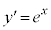 より、
より、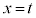 における接線の方程式は、
における接線の方程式は、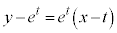
これが原点を通るとき、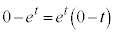
∴ 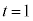
このとき接線の傾きはe
従って、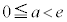 のときは、直線と
のときは、直線と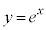 は交わらず、解は0個。
は交わらず、解は0個。
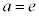 のときは、直線と
のときは、直線と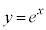 が接するので、解は1個。
が接するので、解は1個。
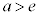 のときは、直線と
のときは、直線と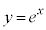 は2交点もつので、解は2個。
は2交点もつので、解は2個。
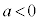 のとき1個、
のとき1個、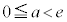 のとき0個、
のとき0個、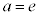 のとき1個、
のとき1個、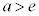 のとき2個。......[答]
のとき2個。......[答]
 [解法2] 定数の分離という技巧を用います。ここでは、定数aを分離するために、与方程式をxで割ります。xで割るときに、
[解法2] 定数の分離という技巧を用います。ここでは、定数aを分離するために、与方程式をxで割ります。xで割るときに、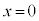 という解があるかも知れない、という点に注意します。
という解があるかも知れない、という点に注意します。
与方程式に、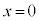 を代入しても成り立たないので、
を代入しても成り立たないので、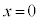 は解ではありません。よって、xで割ると、
は解ではありません。よって、xで割ると、
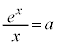
という形の方程式になりますが、これを、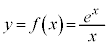 と
と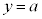 との連立方程式と見れば、
との連立方程式と見れば、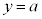 のグラフはx軸に平行な直線で、これと
のグラフはx軸に平行な直線で、これと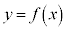 のグラフの交点の数を考えるのは容易です。
のグラフの交点の数を考えるのは容易です。
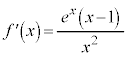 ,
,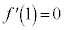 ,
,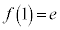 より、増減表は以下の通りで、
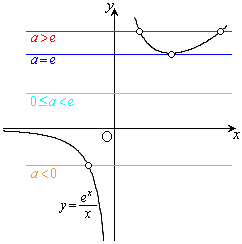
より、増減表は以下の通りで、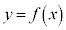 のグラフは右図。
のグラフは右図。
グラフより、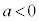 のとき1個、
のとき1個、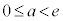 のとき0個、
のとき0個、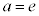 のとき1個、
のとき1個、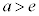 のとき2個。......[答]
のとき2個。......[答]
定数を分離することにより、グラフはやや複雑になりますが、解の個数を数えやすくなります。
例2.方程式: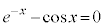 (
(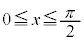 )の解の個数は、
)の解の個数は、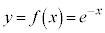 ,
,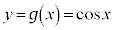 の連立と見ると、
の連立と見ると、
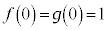 ,
,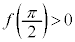 ,
,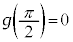 であり、
であり、
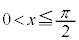 において、
において、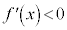 ,
,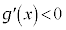 で、ともに単調減少ですが、
で、ともに単調減少ですが、
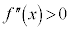 ,
,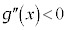 より、
より、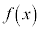 は下に凸、
は下に凸、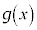 は上に凸なので、
は上に凸なので、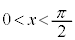 にも、
にも、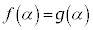 となるαが存在すると断定できます。
となるαが存在すると断定できます。
従って、解の個数は2個です。
しかし、以下のように、ある区間で凹凸まで一致してしまう場合には、精密に調べる必要が出てきます。
例3.方程式: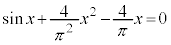 (
(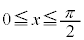 )の解の個数を調べます。
)の解の個数を調べます。
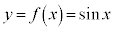 ,
,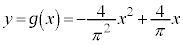 の連立と見ると、
の連立と見ると、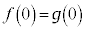 ,
,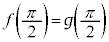
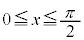 において、
において、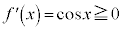 ,
,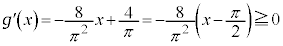 で、ともに単調増加。
で、ともに単調増加。
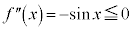 ,
,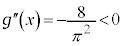 で、ともに上に凸です。
で、ともに上に凸です。
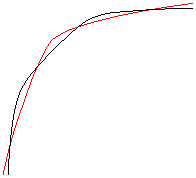 このような場合には、
このような場合には、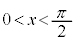 において、解の有無を単純に考えることはできません。右図のように、2つのグラフが絡み合うような可能性があるからです。
において、解の有無を単純に考えることはできません。右図のように、2つのグラフが絡み合うような可能性があるからです。
この問題では、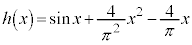 を丁寧に調べる必要があります。
を丁寧に調べる必要があります。
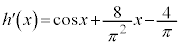
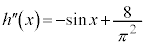
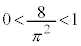 なので、
なので、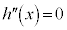 は、
は、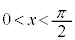 の範囲にただ1つの解をもちます。これをαとします。
の範囲にただ1つの解をもちます。これをαとします。
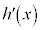 の増減表は、
の増減表は、
増減表より、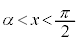 において、
において、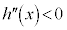 なので、
なので、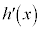 は単調減少です。
は単調減少です。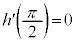 より、
より、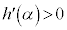 です。
です。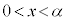 では、
では、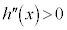 なので、
なので、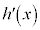 は単調増加です。
は単調増加です。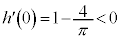 ,
,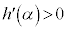 より、
より、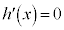 は、
は、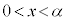 の範囲にただ1つの解をもちます。これをβとします。
の範囲にただ1つの解をもちます。これをβとします。
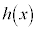 の増減表は、
の増減表は、
増減表より、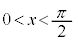 において、
において、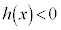 です。
です。
よって、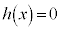 は、
は、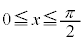 の範囲に、0と
の範囲に、0と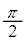 の2個の解をもちます。
の2個の解をもちます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 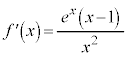 ,
,