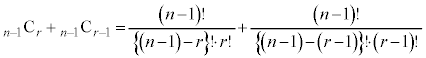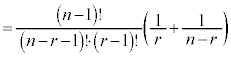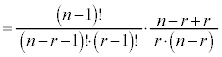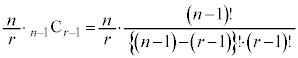組み合わせ 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
異なるn個のものから異なるr個を選ぶ組み合わせの数は、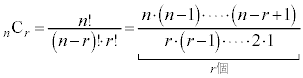 通り。
通り。
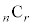 記号ですが、分子には、nから1ずつ減りながら連続r個の積が来ます。分母には
記号ですが、分子には、nから1ずつ減りながら連続r個の積が来ます。分母には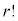 が来ます。
が来ます。
例えば、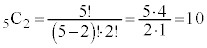 です。
です。
特に、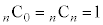 ,
,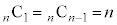 です。
です。
異なるn個のものから異なるr個を選んで並べる方法の数は、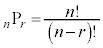 通りあります。
通りあります。
r個のものを並べる並べ方は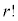 通りありますが、並べ方を変えても選び方としては共通なので、1通りの選び方について
通りありますが、並べ方を変えても選び方としては共通なので、1通りの選び方について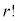 通りの並べ方があることになります。
通りの並べ方があることになります。
従って、異なるn個のものから異なるr個を選ぶ方法の数は、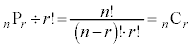 通りとなります。
通りとなります。
例えば、8人の生徒から、清掃係を3人選ぶ選び方は、 通りあります。
通りあります。
C記号には以下の重要性質があります。
(1) 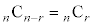
(2) 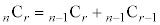
(3) 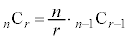
[証明] (1) 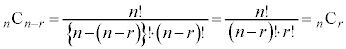
(2) 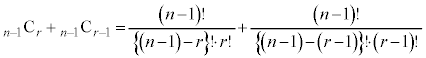
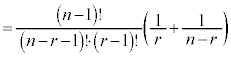
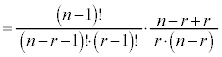
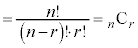
(3) 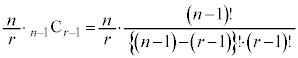
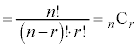 (証明終)
(証明終)
性質(1)により、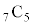 は、
は、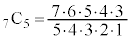 と計算せずに、
と計算せずに、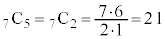 と計算します。
と計算します。
性質(2)は、異なるn個からr個を選ぶときに、まず、ある1個Aを選ぶか選ばないかに分け、Aを選ばないときにはA以外の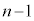 個の中からr個選び、Aを選ぶときにはA以外の
個の中からr個選び、Aを選ぶときにはA以外の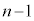 個の中から
個の中から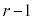 個を選んでAと合わせてr個を選ぶ、と、考えることもできる、ということを意味しています。
個を選んでAと合わせてr個を選ぶ、と、考えることもできる、ということを意味しています。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 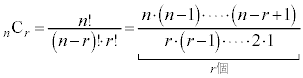 通り。
通り。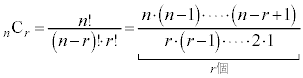 通り。
通り。