複素数 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
2次方程式の解の判別
2次方程式: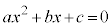 の解は、
の解は、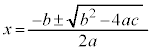 であるが、判別式:
であるが、判別式: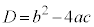 (2次方程式の解の根号内をDとした)が、
(2次方程式の解の根号内をDとした)が、
1) 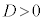 のときは、異なる2つの実数解
のときは、異なる2つの実数解
2) 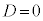 のときは、重解(実数解)
のときは、重解(実数解)
3) 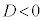 のときは、
のときは、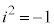 をみたす数iを導入して、
をみたす数iを導入して、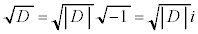 とし、このときも、異なる2つの解をもつ、ということにする。
とし、このときも、異なる2つの解をもつ、ということにする。
iを用いて、2次方程式の解を、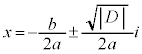 (
(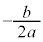 ,
,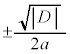 は実数である)と書くことができる。
は実数である)と書くことができる。
虚数、複素数
上記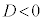 の場合の2次方程式の解のような、
の場合の2次方程式の解のような、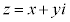 (x,yは実数で
(x,yは実数で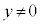 ,
,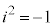 )という形の数を虚数という。iを虚数単位という。
)という形の数を虚数という。iを虚数単位という。
上記の2次方程式の3)の場合の解を虚数解という。
即ち、2次方程式の判別式Dが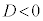 となるときには、2次方程式は異なる2つの虚数解をもつ。
となるときには、2次方程式は異なる2つの虚数解をもつ。
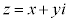 (x,yは実数,
(x,yは実数,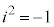 )は、
)は、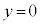 のとき
のとき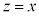 で実数になり、
で実数になり、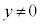 のとき虚数になる。特に、
のとき虚数になる。特に、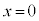 で
で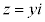 という形になるとき、純虚数と言う。
という形になるとき、純虚数と言う。
実数と虚数を合わせて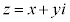 (x,yは実数,
(x,yは実数,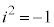 )と書ける数を複素数という。
)と書ける数を複素数という。
xを複素数zの実部といい、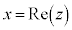 と書く。
と書く。
yを複素数zの虚部といい、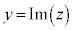 と書く。
と書く。
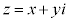 に対して、
に対して、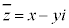 をzの共役複素数という。
をzの共役複素数という。
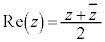 ,
,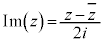 である。
である。
[例] 2次方程式: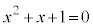 の判別式は
の判別式は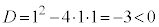 だから、実数解をもたない。
だから、実数解をもたない。
解は、虚数となり、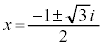
2解の実部はともに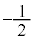 ,虚部は
,虚部は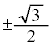
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 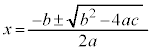 であるが、
であるが、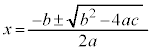 であるが、判別式:
であるが、判別式: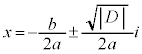 (
(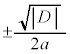 は実数である)と書くことができる。
は実数である)と書くことができる。