���f���̐}�`�I���p�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���f���̐}�`�I���p���l���܂��B
[��1]�@�Ȃ��p�F�قȂ�3�_ �C
�C �C
�C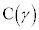 �ɑ��A
�ɑ��A �ł��B
�ł��B
 �C
�C �C
�C �ɑ��A
�ɑ��A �����߂܂��B
�����߂܂��B

����āA
[��2]�@���p�ӎO�p�`�̏����F3�_ �C
�C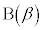 �C
�C ���A
���A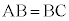 �C
�C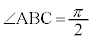 �ƂȂ钼�p�ӎO�p�`���Ȃ����������߂܂��B
�ƂȂ钼�p�ӎO�p�`���Ȃ����������߂܂��B
 ���
��� �C
�C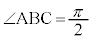 ���
���
 ���A
���A ��
�� 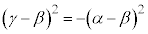
����āA
[��3]�@���O�p�`�̏����F3�_ �C
�C �C
�C �����O�p�`���Ȃ����������߂܂��B
�����O�p�`���Ȃ����������߂܂��B
AB=BC���� �ł��邱�Ƃ������ł��B���Ȃ킿�A
�ł��邱�Ƃ������ł��B���Ȃ킿�A ���A
���A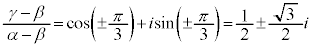
 �Ƃ����ƁA
�Ƃ����ƁA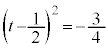 �@��
�@�� 
����āA ���A
���A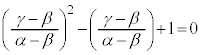
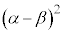 �������āA
�������āA
�W�J���Đ�������ƁA
[��4]�@�꒼����ɂ�������F�قȂ�3�_ �C
�C �C
�C ���꒼����ɂ�����������߂܂��B
���꒼����ɂ�����������߂܂��B
A�CB�CC�����̏��Ɉ꒼����ɕ��ԂƂ� �CB�CA�CC�����̏��Ɉ꒼����ɕ��ԂƂ�
�CB�CA�CC�����̏��Ɉ꒼����ɕ��ԂƂ�
������A ��
��  �͎��� ��
�͎��� �� 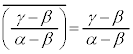
������āA
�W�J���Đ�������ƁA
[��5]�@���s�����E���������F�قȂ�4�_ �C
�C �C
�C �C
�C �ɑ��āA
�ɑ��āA
�EAB // CD �� 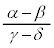 ������ ��
������ �� 
�EAB �� CD ��  ��
�� 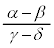 �������� ��
�������� �� 
[��6]�@���Ώ̂ȓ_�F���_O�Ɠ_ �����Ԓ����Ɋւ��ē_
�����Ԓ����Ɋւ��ē_ �ƑΏ̂ȓ_
�ƑΏ̂ȓ_ �����߂܂��B
�����߂܂��B
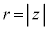 �C
�C �Ƃ��āA����OP�Cα�Cβ�����_O�̉��ɔ����v���Ɋp
�Ƃ��āA����OP�Cα�Cβ�����_O�̉��ɔ����v���Ɋp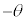 ��]������ƁA�����A
��]������ƁA�����A �C
�C �ɗ��܂����A�����Ɋւ��đΏ̂ȓ_�݂͌��ɋ����ȕ��f���ɂȂ�̂ŁA
�ɗ��܂����A�����Ɋւ��đΏ̂ȓ_�݂͌��ɋ����ȕ��f���ɂȂ�̂ŁA

���ӂ�r�������āA ���A
���A �@��
�@�� 
�Ⴆ�A���_O�Ɠ_P �����Ԓ����Ɋւ��ē_A
�����Ԓ����Ɋւ��ē_A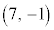 �ƑΏ̂ȓ_B�����߂�ƁA
�ƑΏ̂ȓ_B�����߂�ƁA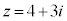 �C
�C �Ƃ��āA
�Ƃ��āA

����āAB
[��7]�@�~�F (
( )����z�́Aα�𒆐S�Ƃ��锼�ar�̉~����`���܂��B
)����z�́Aα�𒆐S�Ƃ��锼�ar�̉~����`���܂��B
 �Ƃ����`�̎�������Ƃ��A�܂��A
�Ƃ����`�̎�������Ƃ��A�܂��A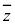 �ł�����ƁA
�ł�����ƁA
����� �ł������悤�ɕό`���āA
�ł������悤�ɕό`���āA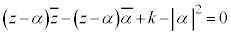
 �@��
�@�� 
���̎��́A �̂Ƃ��Aα�𒆐S�Ƃ��锼�a
�̂Ƃ��Aα�𒆐S�Ƃ��锼�a �̉~����`���܂��B
�̉~����`���܂��B
�Ⴆ�� �Ƃ��āA�_
�Ƃ��āA�_ �܂ł̋����Ɠ_
�܂ł̋����Ɠ_
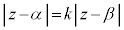
[��8]�@�ϊ��F�P�ʉ~ ��̓_���A�ϊ�
��̓_���A�ϊ� (
( �͕��f��)�@����@�@�ɂ���Ĉڂ�}�`�����߂܂��B
�͕��f��)�@����@�@�ɂ���Ĉڂ�}�`�����߂܂��B �Ƃ��܂��B
�Ƃ��܂��B
�@��z�ɂ��ĉ����ƁA
 �C
�C �@��
�@�� 
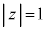 �ɑ������ƁA
�ɑ������ƁA �@���@
�@���@
���̎��́A�_w�Ɠ_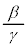 �Ƃ̋����ƁA�_w�Ɠ_α�Ƃ̋����̔䂪1�F
�Ƃ̋����ƁA�_w�Ɠ_α�Ƃ̋����̔䂪1�F �ł��邱�Ƃ��Ӗ����܂��B
�ł��邱�Ƃ��Ӗ����܂��B
�E �̂Ƃ��A�_w�́A�_
�̂Ƃ��A�_w�́A�_ �Ɠ_α�̐���������̓_�ɂȂ�܂��B
�Ɠ_α�̐���������̓_�ɂȂ�܂��B
�E �̂Ƃ��A�_w�́A�_
�̂Ƃ��A�_w�́A�_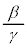 �Ɠ_α��1�F
�Ɠ_α��1�F �̔�ɓ�������_
�̔�ɓ�������_ ��1�F
��1�F �̔�ɊO������_
�̔�ɊO������_ �a�̗��[�Ƃ���~(�A�|���j�E�X�̉~)����̓_�ɂȂ�܂��B
�a�̗��[�Ƃ���~(�A�|���j�E�X�̉~)����̓_�ɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �ł��B
�ł��B �ł��B
�ł��B



 ���A
���A ���A
���A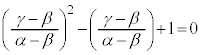
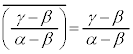




 �@���@
�@���@
 ��1�F
��1�F �a�̗��[�Ƃ���~(�A�|���j�E�X�̉~)����̓_�ɂȂ�܂��B
�a�̗��[�Ƃ���~(�A�|���j�E�X�̉~)����̓_�ɂȂ�܂��B