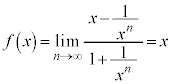関数の連続 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
関数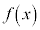 が
が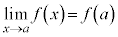 を満たすとき、
を満たすとき、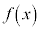 は
は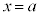 において連続である、と言う。連続でないとき、
において連続である、と言う。連続でないとき、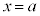 において不連続であると言う。
において不連続であると言う。
関数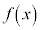 が、
が、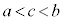 を満たす全ての実数cについて、
を満たす全ての実数cについて、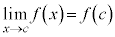 を満たすとき、
を満たすとき、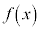 は開区間
は開区間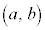 において連続である、と言う。
において連続である、と言う。
閉区間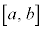 で定義された関数
で定義された関数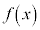 が、開区間
が、開区間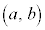 で連続で、
で連続で、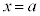 ,
,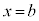 において、
において、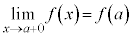 ,
,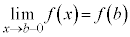 を満たせば、
を満たせば、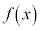 は
は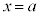 ,
,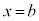 において連続であり、閉区間
において連続であり、閉区間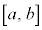 で連続な関数である。
で連続な関数である。
定義域内のすべてのxにおいて連続な関数を連続関数と言う。
ある区間で連続な関数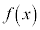 ,
,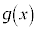 があるとき、k,hを実数として、
があるとき、k,hを実数として、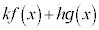 ,
,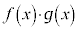 も連続である。その区間内で
も連続である。その区間内で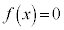 となるxを除いて、
となるxを除いて、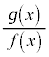 も連続である。
も連続である。
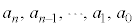 を実数だとして、
を実数だとして、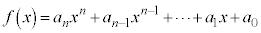 は、全実数において連続な関数です。
は、全実数において連続な関数です。
aを実数だとして、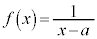 は
は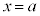 において不連続、
において不連続、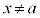 において連続な関数です。
において連続な関数です。
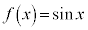 ,
,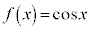 ,
,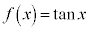 ,
,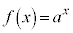 (
(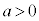 かつ
かつ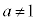 )は、全実数において連続な関数です。
)は、全実数において連続な関数です。
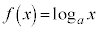 (
(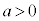 かつ
かつ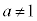 )は、
)は、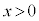 において連続な関数です。
において連続な関数です。
aを実数だとして、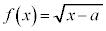 は、
は、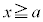 において連続な関数です。
において連続な関数です。
例1.xを越えない最大の整数を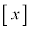 で表します。この記号
で表します。この記号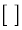 をガウスの記号と言います。
をガウスの記号と言います。 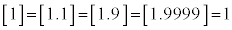 ,
,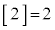 です。
です。
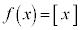 という関数は、
という関数は、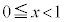 において
において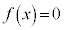 ,
,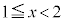 において
において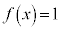 ,
,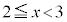 において
において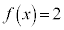 という値をとりますが、
という値をとりますが、
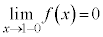 ,
,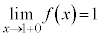 より、
より、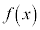 は
は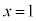 において不連続です。
において不連続です。
また、kを整数として、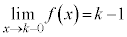 ,
,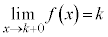 より、
より、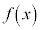 は
は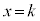 において不連続です。
において不連続です。
例2.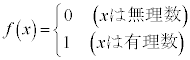 という関数は、いかなる無理数と無理数の間にも有理数があり、いかなる有理数と有理数の間にも無理数があるので、至るところ不連続な関数です。
という関数は、いかなる無理数と無理数の間にも有理数があり、いかなる有理数と有理数の間にも無理数があるので、至るところ不連続な関数です。
例3.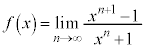 という関数は、
という関数は、
 ・
・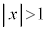 のとき、
のとき、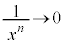 より、
より、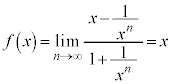
・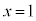 のとき、
のとき、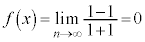
・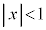 のとき、
のとき、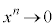 より、
より、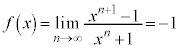
・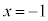 のとき、nが奇数なら
のとき、nが奇数なら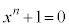 で、
で、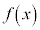 の値が定義できません。
の値が定義できません。
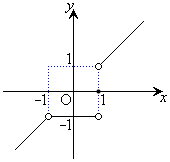
グラフを描くと右図のようになり、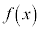 は、
は、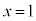 ,
,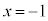 において、不連続です。
において、不連続です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 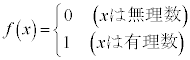 という関数は、いかなる無理数と無理数の間にも有理数があり、いかなる有理数と有理数の間にも無理数があるので、至るところ不連続な関数です。
という関数は、いかなる無理数と無理数の間にも有理数があり、いかなる有理数と有理数の間にも無理数があるので、至るところ不連続な関数です。