対偶

対偶　　　関連問題

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

条件A，条件Bがあって、命題P：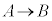

に対して、命題Q：

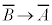を、命題Pの対偶と言う。

，

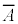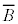は、それぞれ、条件A，Bの否定を意味する。

ある学校のあるクラスで生徒にアンケートをとってみたところ次のことがわかりました。アンチ巨人の人はひどい話だと怒るかも知れませんが、あるクラスでの話です。

スポーツの中で野球を一番好きだと答えた生徒が全員、巨人ファンだったのです。

ですが、巨人ファンであっても、サッカーの方が好き、アメフットの方が好き、などという生徒もいました。このとき(“→”は、”ならば”と読んでください)、
　　　命題※：野球愛好家である→巨人ファンである
が成立します。ですが、
　　　命題：巨人ファンである→野球愛好家である
は成立しません。

ついでに言っておくと、命題※の「野球愛好家である」という条件を「巨人ファンである」ための十分条件と言います。「野球愛好家である」ことが「巨人ファンである」ことの十分に厳しい条件だと思ってください。
これに対して、「巨人ファンである」という条件を「野球愛好家である」ことの必要条件と言います。「巨人ファンである」ことが「野球ファンである」ことの必要最低限の条件だと思ってください。

話を元に戻して、このクラスでは、
　　　命題：巨人ファンではない→野球愛好家ではない
が成立します。
この、「巨人ファンではない→野球愛好家ではない」という命題を、「野球愛好家である→巨人ファンである」という命題の、「対偶」と言います。対偶は元の命題の言い換えに過ぎません。

証明問題によっては、問題文に書いてある通りに証明するよりも、対偶を考えた方が証明しやすい場合があります。

例．命題「整数nの2乗が偶数なら、整数nは偶数」の証明
「整数nは偶数」の否定は「整数nは奇数」、「整数nの2乗が偶数」の否定は「整数nの2乗は奇数」なので、「整数nの2乗が偶数なら、整数nは偶数」の対偶は、「整数nが奇数であれば、整数nの2乗は奇数」です。対偶を証明すると、

整数nが奇数であれば、mを整数として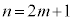

とおくことができます。このとき、

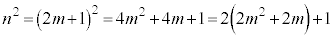は奇数です。(証明終)

これで、元の命題も証明されたことになります。

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

　　数学基礎事項TOP　　数学TOP　　TOPページに戻る

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。

【広告】広告はここまでです。

苦学楽学塾 随時入会受付中！
理系大学受験ネット塾苦学楽学塾
(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。