剰余類 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
整数nを自然数mで割るとき、商がs,余りがrだとします。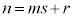 です。
です。
ここで、余りrはm以上にはならず、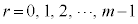 のどれかです。
のどれかです。
つまり、整数の集合をZ,mで割ったとき、余りが0となる整数の集合を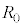 ,余りが1となる整数の集合を
,余りが1となる整数の集合を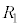 ,・・・,余りが
,・・・,余りが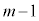 となる整数の集合を
となる整数の集合を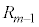 とすると、
とすると、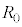 ,
,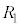 ,・・・,
,・・・,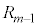 のどの2つ
のどの2つ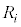 ,
,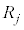 (
(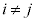 ,
,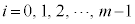 ,
,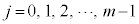 )をとっても、
)をとっても、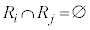 であるとともに、
であるとともに、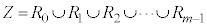 です。
です。
この性質により、全ての整数をm通りに分類することができます。全ての整数に関する性質であっても、全ての整数に対して考える必要はなく、m通りの分類について考えれば十分です。
[例1] 3個の整数x,y,zに対して、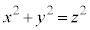 が成り立つとき、x,yのどちらかは3で割りきれることを証明します。
が成り立つとき、x,yのどちらかは3で割りきれることを証明します。
全ての整数は、3で割った商をs,余りをr (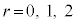 )として、
)として、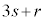 の形に書けます。
の形に書けます。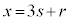 として、
として、
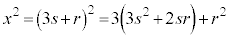
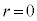 のとき
のとき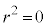 ,
,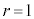 のとき
のとき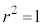
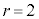 のとき
のとき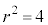 で
で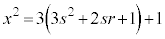
つまり、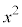 を3で割ると、2余るということはありません。
を3で割ると、2余るということはありません。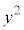 ,
,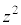 についても3で割ると2余ることはありません。
についても3で割ると2余ることはありません。
x,yがともに3で割り切れないと仮定すると、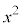 も
も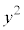 もともに3で割ると1余るので、
もともに3で割ると1余るので、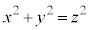 を3で割ると2余ります。これは、
を3で割ると2余ります。これは、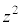 は3で割ると2余ることがない、ことに矛盾します。よって、x,yがともに3で割り切れない、とした仮定は誤りで、x,yのどちらかは3で割りきれます。 (証明終)
は3で割ると2余ることがない、ことに矛盾します。よって、x,yがともに3で割り切れない、とした仮定は誤りで、x,yのどちらかは3で割りきれます。 (証明終)
[例2] 整数の3乗、あるいは、整数の3乗に1を加えるか引くかした整数のいずれかは9で割りきれることを証明します。
整数を、3で割った商をs,余りをr (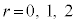 )として、
)として、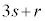 と書くと、
と書くと、
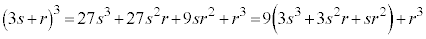
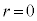 のとき、
のとき、
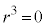 なので、
なので、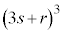 は9で割り切れます。
は9で割り切れます。
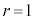 のとき、
のとき、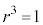 なので、
なので、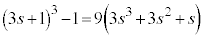 は9で割り切れます。
は9で割り切れます。
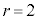 のとき、
のとき、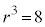 なので、
なので、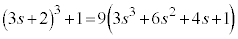 は9で割り切れます。
は9で割り切れます。
これで全ての場合を尽くしました。 (証明終)
nを自然数mで割って余りがrであることを、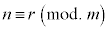 と表す(「nはmを法としてrと合同である」と読みます)記法があります。これを合同式と言います。答案を簡潔に書くのに便利です。なお、rは
と表す(「nはmを法としてrと合同である」と読みます)記法があります。これを合同式と言います。答案を簡潔に書くのに便利です。なお、rは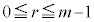 に限りません。
に限りません。
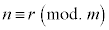 ⇔
⇔ 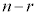 はmの倍数
はmの倍数
です。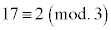 ,
,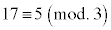 ,
,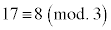 ,
,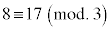 ,すべて正しい合同式です。sを整数として、
,すべて正しい合同式です。sを整数として、
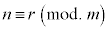 ⇔
⇔ 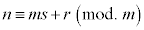 ⇔
⇔ 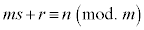
です。なお、合同式には、以下の性質があります。
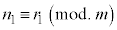 ,
,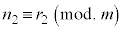 ,kを自然数とするとき、
,kを自然数とするとき、
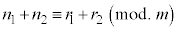 ,
,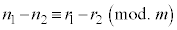 ,
,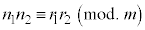 ,
,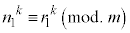 ・・・(*)
・・・(*)
合同式を用いて、[例1]を証明すると、
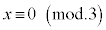 のとき、
のとき、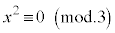
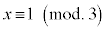 のとき、
のとき、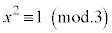
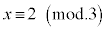 のとき、
のとき、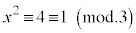
x,yがともに3で割り切れないと仮定すると、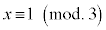 ,または、
,または、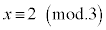 ですが、このとき、
ですが、このとき、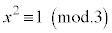
同様に、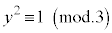 ,
,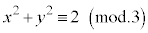 となりますが、
となりますが、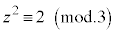 とはなり得ず、
とはなり得ず、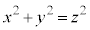 が成立しません。よって、仮定は誤りで、x,yのどちらかは3で割りきれます。 (証明終)
が成立しません。よって、仮定は誤りで、x,yのどちらかは3で割りきれます。 (証明終)
のように、簡潔に答案を書くことができます。
[例2]のように、mod.3とmod.9が両方出てくる場合には、(*)のようには行かないので、mod.9に統一して答案を書く必要があります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。