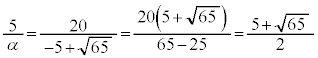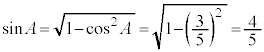共通テスト数学IA '21年第1問
[1] cを正の整数とする。xの2次方程式
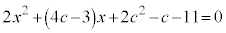 ・・・①
・・・①について考える。
(1) 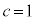 のとき、①の左辺を因数分解すると
のとき、①の左辺を因数分解すると であるから、①の解は
である。
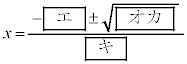
(2) 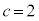 のとき、①の解は
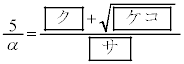
のとき、①の解は であり、大きい方の解をαとすると
である。また、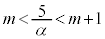 を満たす整数mは
を満たす整数mは である。
である。 (3) 太郎さんと花子さんは、①の解について考察している。
太郎:①の解はcの値によって、ともに有理数である場合もあれば、ともに無理数である場合もあるね。cがどのような値のときに、解は有理数になるのかな。
花子:2次方程式の解の公式の根号の中に着目すればいいんじゃないかな。
①の解が異なる二つの有理数であるような正の整数cの個数は 個である。
個である。
[2] 右の図のように、△ABCの外側に辺AB,BC,CAをそれぞれ1辺とする正方形ADEB,BFGC,CHIAをかき、2点EとF,GとH,IとDをそれぞれ線分で結んだ図形を考える。以下において
とする。
(1) 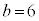 ,
,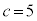 ,
,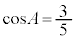 のとき、
のとき、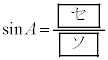 であり、△ABCの面積は
であり、△ABCの面積は ,△AIDの面積は
,△AIDの面積は である。
である。 (2) 正方形BFGC,CHIA,ADEBの面積をそれぞれ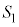 ,
,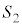 ,
,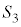 とする。このとき、
とする。このとき、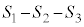 は、
は、 ・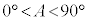 のとき、
のとき、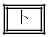 。
。 ・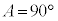 のとき、
のとき、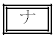 。
。 ・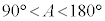 のとき、
のとき、 。
。 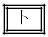 ~
~ の解答群(同じものを繰り返し選んでよい。)
の解答群(同じものを繰り返し選んでよい。) 0である。
0である。 正の値である。
正の値である。 負の値である。
負の値である。 正の値も負の値もとる。
正の値も負の値もとる。(3) △AID,△BEF,△CGHの面積をそれぞれ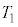 ,
,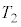 ,
,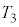 とする。このとき、
とする。このとき、 である。
である。  の解答群
の解答群 a,b,cの値に関係なく、
a,b,cの値に関係なく、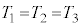
(4) △ABC,△AID,△BEF,△CGHのうち、外接円の半径が最も小さいものを求める。
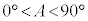 のとき、ID
のとき、ID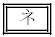 BCであり
BCであり(△AIDの外接円の半径) (△ABCの外接円の半径)
(△ABCの外接円の半径) であるから、外接円の半径が最も小さい三角形は
・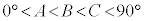 のとき、
のとき、 である。
である。 ・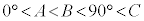 のとき、
のとき、 である。
である。 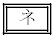 ,
, の解答群(同じものを繰り返し選んでもよい。)
の解答群(同じものを繰り返し選んでもよい。) ,
, の解答群(同じものを繰り返し選んでもよい。)
の解答群(同じものを繰り返し選んでもよい。)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 この問題を正確かつ迅速に仕上げないと、第2問以降の圧倒的迫力に茫然自失することになります。[2](4)は図をきちんと書けば答がわかってしまう?
ア 2 イ 5 ウ 2 ......[答]
エ 5 オカ 65 キ 4 ......[答]
大きい方の解αは、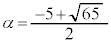
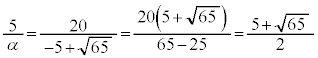
ク 5 ケコ 65 サ 2 ......[答]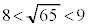 より
より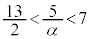 よって、
よって、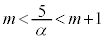 を満たす整数mは、
を満たす整数mは、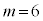
シ 6 .....[答] (3) 会話の中のヒントに書かれていますが、解の公式の根号内(判別式)に着目します。判別式Dは、
異なる二つの有理数解を持つ、ということは、異なる二つの実数解をもつので、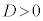 より
より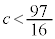 ,cは正の整数なので、
,cは正の整数なので、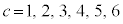 に限られます。このうち、有理数解となるためにDが平方数になるのは、
に限られます。このうち、有理数解となるためにDが平方数になるのは、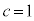 のとき
のとき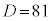 ,
,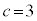 のとき
のとき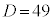 ,
,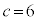 のとき
のとき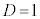 の3個です。
の3個です。
ス 3 ......[答]
セ 4 ソ 5 ......[答]△ABCの面積は、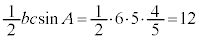
タチ 12 ......[答]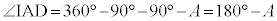 より、△AIDの面積は、
より、△AIDの面積は、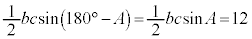
ツテ 12 ......[答] (2) 余弦定理より、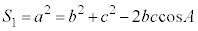
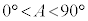 のとき、
のとき、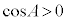 より、
より、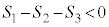
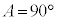 のとき、
のとき、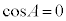 とり、
とり、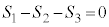
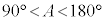 のとき、
のとき、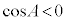 より、
より、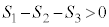
ト 2 ナ 0 ニ 1 ......[答](3) △ABCの外接円の半径をRとして、正弦定理より、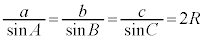 ∴
∴ 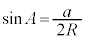 ,
,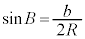 ,
,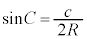
(1)で見たように、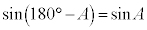 などにより、
などにより、 よって、a,b,cの値に関係なく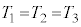
ヌ 3 ......[答] (4) 余弦定理より、
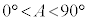 においては
においては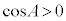 より、
より、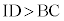 ・・・②
・・・②
△AID,△ABCの外接円の半径は、正弦定理より、それぞれ、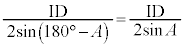 ,
,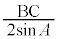 です。よって②より、
です。よって②より、(△AIDの外接円の半径)>(△ABCの外接円の半径)
ネ 2 ノ 2 ......[答]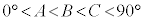 より、
より、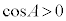 ,
,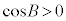 ,
,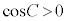
②と同様に、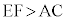 ,
,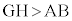
(△BEFの外接円の半径)>(△ABCの外接円の半径)
(△CGHの外接円の半径)>(△ABCの外接円の半径)
外接円の半径が最も小さい三角形は、△ABCです。
ハ 0 ......[答]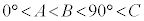 のとき、
のとき、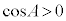 ,
,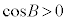 なので、②と同様に、
なので、②と同様に、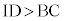 ,
,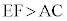 ,よって、
,よって、 (△AIDの外接円の半径)>(△ABCの外接円の半径)
(△BEFの外接円の半径)>(△ABCの外接円の半径)
一方、余弦定理より、
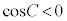 なので、
なので、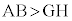 ,△ABC,△CGHの外接円の半径は、正弦定理より、それぞれ、
,△ABC,△CGHの外接円の半径は、正弦定理より、それぞれ、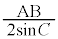 ,
,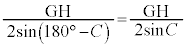
(△ABCの外接円の半径)>(△CGHの外接円の半径)
外接円の半径が最も小さい三角形は、△CGHです。
ヒ 3 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
 であり、△ABCの面積は
であり、△ABCの面積は