�@���ʃe�X�g���wIA '21�N��2��@
[1]�@���㋣�Z�̒Z����100m���ł́A100m�𑖂�̂ɂ����鎞��(�ȉ��A�^�C���ƌĂ�)�́A1��������̐i�ދ���(�ȉ��A�X�g���C�h�ƌĂ�)��1�b������̕���(�ȉ��A�s�b�`�ƌĂ�)�ɊW������B�X�g���C�h�ƃs�b�`�͂��ꂼ��ȉ��̎��ŗ^������B
�������A100m�𑖂�̂ɂ������������́A�Ō��1�����S�[�����C�����܂������Ƃ�����̂ŁA�����ŕ\�����B�ȉ��A�P�ʂ͕K�v�̂Ȃ�����ȗ�����B
�Ⴆ�A�^�C����10.81�ŁA���̂Ƃ��̕�����48.5�ł������Ƃ��A�X�g���C�h��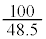 ����2.06�C�s�b�`��
����2.06�C�s�b�`��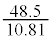 ����4.49�ł���B
����4.49�ł���B
�Ȃ��A�����̌`�ʼn���ꍇ�́A��̒����ɂ���悤�ɁA�w�肳�ꂽ�����̈���̌����l�̌ܓ����ē�����B�܂��A�K�v�ɉ����āA�w�肳�ꂽ���܂� �Ƀ}�[�N����B
�Ƀ}�[�N����B (1) �X�g���C�h��x�C�s�b�`��z�Ƃ����B�s�b�`��1�b������̕����A�X�g���C�h��1��������̐i�ދ����Ȃ̂ŁA1�b������̐i�ދ������Ȃ킿���ϑ��x�́Ax��z��p���� (m/�b)�ƕ\�����B
(m/�b)�ƕ\�����B ������A�^�C���ƁA�X�g���C�h�A�s�b�`�Ƃ̊W��
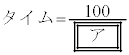 �@����@
�@����@�ƕ\�����̂ŁA ���ő�ɂȂ�Ƃ��Ƀ^�C�����ł��悭�Ȃ�B�������A�^�C�����悭�Ȃ�Ƃ́A�^�C���̒l���������Ȃ邱�Ƃł���B
���ő�ɂȂ�Ƃ��Ƀ^�C�����ł��悭�Ȃ�B�������A�^�C�����悭�Ȃ�Ƃ́A�^�C���̒l���������Ȃ邱�Ƃł���B
 �̉Q
�̉Q  �@
�@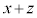 �@�@�@
�@�@�@ �@
�@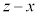 �@�@�@
�@�@�@ �@
�@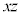
 �@
�@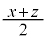 �@�@�@
�@�@�@ �@
�@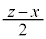 �@�@�@
�@�@�@ �@
�@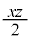
(2) �j�q�Z����100m���̑I��ł��鑾�Y����́A�@�ɒ��ڂ��āA�^�C�����ł��悭�Ȃ�X�g���C�h�ƃs�b�`���l���邱�Ƃɂ����B
���̕\�́A���Y�����K��100m��3�����Ƃ��̃X�g���C�h�ƃs�b�`�̃f�[�^�ł���B
| �@ | 1��� | 2��� | 3��� |
| �X�g���C�h | 2.05 | 2.10 | 2.15 |
| �s�b�` | 4.70 | 4.60 | 4.50 |
�܂��A�X�g���C�h�ƃs�b�`�ɂ͂��ꂼ����E������B���Y����̏ꍇ�A�X�g���C�h�̍ő�l��2.40�C�s�b�`�̍ő�l��4.80�ł���B
���Y����́A��̕\����A�X�g���C�h��0.05�傫���Ȃ�ƃs�b�`��0.1�������Ȃ�Ƃ����W������ƍl���āA�s�b�`���X�g���C�h��1�����ŕ\�����Ɖ��肵���B���̂Ƃ��A�s�b�`z�̓X�g���C�hx��p����
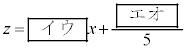 �@����A
�@����A�ƕ\�����B
�A�����Y����̃X�g���C�h�̍ő�l2.40�ƃs�b�`�̍ő�l4.80�܂Ő��藧�Ɖ��肷��ƁAx�̒l�͈͎̔͂��̂悤�ɂȂ�B
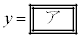 �Ƃ����B�A��
�Ƃ����B�A��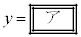 �ɑ�����邱�Ƃɂ��Ay��x�̊��Ƃ��ĕ\�����Ƃ��ł���B���Y����̃^�C�����ł��悭�Ȃ�X�g���C�h�ƃs�b�`�����߂邽�߂ɂ́A
�ɑ�����邱�Ƃɂ��Ay��x�̊��Ƃ��ĕ\�����Ƃ��ł���B���Y����̃^�C�����ł��悭�Ȃ�X�g���C�h�ƃs�b�`�����߂邽�߂ɂ́A �͈̔͂�y�̒l���ő�ɂ���x�̒l��������悢�B���̂Ƃ��Ay�̒l���ő�ɂȂ�̂�
�͈̔͂�y�̒l���ő�ɂ���x�̒l��������悢�B���̂Ƃ��Ay�̒l���ő�ɂȂ�̂� �̂Ƃ��ł���B
�̂Ƃ��ł���B
����āA���Y����̃^�C�����ł��悭�Ȃ�̂́A�X�g���C�h�� �̂Ƃ��ł���A���̂Ƃ��A�s�b�`��
�̂Ƃ��ł���A���̂Ƃ��A�s�b�`��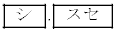 �ł���B�܂��A���̂Ƃ��̑��Y����̃^�C���́A�@�ɂ��
�ł���B�܂��A���̂Ƃ��̑��Y����̃^�C���́A�@�ɂ�� �ł���B
�ł���B
 �ɂ��ẮA�ł��K���Ȃ��̂��A����
�ɂ��ẮA�ł��K���Ȃ��̂��A���� �`
�` �̂��������I�ׁB
�̂��������I�ׁB �@9.68�@�@�@
�@9.68�@�@�@ �@9.97�@�@�@
�@9.97�@�@�@ �@10.09
�@10.09 �@10.33�@�@�@
�@10.33�@�@�@ �@10.42�@�@�@
�@10.42�@�@�@ �@10.55
�@10.55
[2]�@�A�Ǝ҂̏]������Y�Ƃ́A�Ζ����鎖�Ə��̎�Ȍo�ϊ����̎�ނɂ���āA��1���Y��(�_�ƁA�ыƂƋ���)�A��2���Y��(�z�ƁA���ƂƐ�����)�A��3���Y��(�O�L�ȊO�̎Y��)�̎O�ɕ��ނ����B���̘J���̒���(��������)�ł́A47�̓s���{���ʂɑ�1���A��2���A��3�����ꂼ��̎Y�Ƃ��Ƃ̏A�ƎҐ������\����Ă���B�����ł͓s���{���ʂɁA�A�ƎҐ��ɑ���e�Y�ƂɏA�Ƃ���l���̊������Z�o�������̂��A�e�Y�Ƃ́u�A�ƎҐ������v�ƌĂԂ��Ƃɂ���B
(1) �}1�́A1975�N�x����2010�N�x�܂�5�N���Ƃ�8�̔N�x(���ꂼ������_�Ƃ���)�ɂ�����s���{���ʂ̎O�̎Y�Ƃ̏A�ƎҐ������Ђ��}�ŕ\�������̂ł���B�e���_�̔��Ђ��}�́A���ꂼ��ォ�珇�ɑ�1���Y�ƁA��2���Y�ƁA��3���Y�Ƃ̂��̂ł���B
���� �`
�` �̂����A�}1����ǂݎ��邱�ƂƂ����������Ȃ�������
�̂����A�}1����ǂݎ��邱�ƂƂ����������Ȃ������� ��
�� �ł���B
�ł���B
 ��
�� �̉Q(�̏��͖��Ȃ��B)
�̉Q(�̏��͖��Ȃ��B)  �@��1���Y�Ƃ̏A�ƎҊ����̎l���ʔ͈͂́A2000�N�x�܂ł́A��̎��_�ɂȂ�ɂ��������Č������Ă���B
�@��1���Y�Ƃ̏A�ƎҊ����̎l���ʔ͈͂́A2000�N�x�܂ł́A��̎��_�ɂȂ�ɂ��������Č������Ă���B �@��1���Y�Ƃ̏A�ƎҊ����ɂ��āA�����̂Ђ��̒����ƉE���̂Ђ��̒������r����ƁA�ǂ̎��_�ɂ����Ă������̕��������B
�@��1���Y�Ƃ̏A�ƎҊ����ɂ��āA�����̂Ђ��̒����ƉE���̂Ђ��̒������r����ƁA�ǂ̎��_�ɂ����Ă������̕��������B �@��2���Y�Ƃ̏A�ƎҐ������̒����l�́A1990�N�x�ȍ~�A��̎���ɂȂ�ɂ��������Č������Ă���B
�@��2���Y�Ƃ̏A�ƎҐ������̒����l�́A1990�N�x�ȍ~�A��̎���ɂȂ�ɂ��������Č������Ă���B �@��2���Y�Ƃ̏A�ƎҐ������̑�1�l���ʐ��́A��̎��_�ɂȂ�ɂ��������Č������Ă���B
�@��2���Y�Ƃ̏A�ƎҐ������̑�1�l���ʐ��́A��̎��_�ɂȂ�ɂ��������Č������Ă���B �@��3���Y�Ƃ̏A�ƎҐ������̑�3�l���ʐ��́A��̎��_�ɂȂ�ɂ��������đ������Ă���B
�@��3���Y�Ƃ̏A�ƎҐ������̑�3�l���ʐ��́A��̎��_�ɂȂ�ɂ��������đ������Ă���B �@��3���Y�Ƃ̏A�ƎҐ������̍ŏ��l�́A��̎��_�ɂȂ�ɂ��������đ������Ă���B
�@��3���Y�Ƃ̏A�ƎҐ������̍ŏ��l�́A��̎��_�ɂȂ�ɂ��������đ������Ă���B(2)�@(1)�Ŏ��グ��8���_�̒�����5���_�����o���čl����B�e���_�ɂ�����s���{���ʂ́A��1���Y�ƂƑ�3���Y�Ƃ̏A�ƎҐ������̃q�X�ƃO��������̃O���t�ɂ܂Ƃ߂Ă��������̂��A���y�[�W�̌܂̃O���t�ł���B���ꂼ��̉E���̖Ԋ|�������q�X�ƃO��������3���Y�Ƃ̂��̂ł���B�Ȃ��A�q�X�ƃO�����̊e�K���̋�Ԃ́A�����̐��l���܂݁A�E���̐��l���܂܂Ȃ��B
�E1985�N�x�ɂ�����O���t�� �ł���B
�ł���B �E1995�N�x�ɂ�����O���t�� �ł���B
�ł���B  �C
�C �ɂ��ẮA�ł��K���Ȃ��̂��A����
�ɂ��ẮA�ł��K���Ȃ��̂��A���� �`
�` �̂����������I�ׁA�������A�������̂��J��Ԃ��I��ł��悢�B
�̂����������I�ׁA�������A�������̂��J��Ԃ��I��ł��悢�B(3) �O�̎Y�Ƃ�������g�ݍ��킹�ēs���{���ʂ̏A�ƎҐ������̎U�z�}���쐬�����B�}2�̎U�z�}�Q�́A�����珇��1975�N�x�ɂ������1���Y��(����)�Ƒ�2���Y��(�c��)�̎U�z�}�A��2���Y��(����)�Ƒ�3���Y��(�c��)�̎U�z�}�A����ё�3���Y��(����)�Ƒ�1���Y��(�c��)�̎U�z�}�ł���B�܂��A�}3�͓��l�ɍ쐬����2015�N�x�̎U�z�}�Q�ł���B
����(I)�C(II)�C(III)�́A1975�N�x����Ƃ����Ƃ��́A2015�N�x�̕ω����L�q�������̂ł���B�������A�����Łu���ւ������Ȃ����v�Ƃ́A���W���̐�Βl���傫���Ȃ������Ƃ��Ӗ�����B
(I)�@�s���{���ʂ̑�1���Y�Ƃ̏A�ƎҐ������Ƒ�2���Y�Ƃ̏A�ƎҐ������̊Ԃ̑��ւ͋����Ȃ����B
(II)�@�s���{���ʂ̑�2���Y�Ƃ̏A�ƎҐ������Ƒ�3���Y�Ƃ̏A�ƎҐ������̊Ԃ̑��ւ͋����Ȃ����B
(III)�@�s���{���ʂ̑�3���Y�Ƃ̏A�ƎҐ������Ƒ�1���Y�Ƃ̏A�ƎҐ������̊Ԃ̑��ւ͋����Ȃ����B
(I)�C(II)�C(III)�̐���̑g�ݍ��킹�Ƃ��Đ��������̂�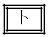 �ł���B
�ł���B (4)�@�e�s���{���̏A�ƎҐ��̓���Ƃ��Ēj���ʂ̏A�ƎҐ������\����Ă���B�����ŁA�A�ƎҐ��ɑ���j���E�����̏A�ƎҐ��̊��������ꂼ��u�j���̏A�ƎҐ������v�A�u�����̏A�ƎҐ������v�ƌĂԂ��Ƃɂ��A������s���{���ʂɎZ�o�����B�}4�́A2015�N�x�ɂ�����s���{���ʂ́A��1���Y�Ƃ̏A�ƎҐ�����(����)�ƁA�j���̏A�ƎҐ�����(�c��)�̎U�z�}�ł���B
�e�s���{���́A�j���̏A�ƎҐ��Ə����̏A�ƎҐ������v����ƏA�ƎҐ��̑S�̂ƂȂ邱�Ƃɒ��ӂ���ƁA2015�N�x�ɂ�����s���{���ʂ́A��1���Y�Ƃ̏A�ƎҐ�����(����)�ƁA�����̏A�ƎҐ�����(�c��)�̎U�z�}��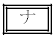 �ł���B
�ł���B
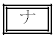 �ɂ��ẮA�ł��K���Ȃ��̂��A����
�ɂ��ẮA�ł��K���Ȃ��̂��A���� �`
�` �̂��������I�ׁB�Ȃ��A�ݖ�̓s���Ŋe�U�z�}�̉����Əc���̖ڐ���͏ȗ����Ă��邪�A�����͉E�����A�c���͏���������ꂼ�ꐳ�̕����ł���B
�̂��������I�ׁB�Ȃ��A�ݖ�̓s���Ŋe�U�z�}�̉����Əc���̖ڐ���͏ȗ����Ă��邪�A�����͉E�����A�c���͏���������ꂼ�ꐳ�̕����ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
��[1]��2�����̉��p���ł����A�����܂ŋÂ�Ȃ��Ă��A�Ƃ����C�����܂��B[2]�́A�u���w�v�̓������Ȃ�ł��傤���H�n�������o���H�Ǝv���Ă��܂��܂��B�ł����A�������ق��āA�ƌ��������Ȃ�قǂɂ������ݖ₪�����A�C���������Đ}�ׂȂ��Ɛ����ł��܂���B
[1](1) �P�ʂɖڂ�t����ƁA�X�g���C�h(m/��)�ƃs�b�`(��/�b)��������A���ϑ��x�̒P��(m/�b)�ɂȂ�̂ŁA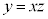 �Ƃ킩��܂��B
�Ƃ킩��܂��B �A�@2 ......[��]
(2) 1��ڂ�2���(���̖��ł́A2��ڂ�3��ڂł�����)�ŁA�X�g���C�h�ɑ���s�b�`�̕ω����́A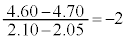 �C
�C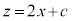 �Ƃ����āA
�Ƃ����āA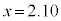 �C
�C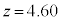 ��������ƁA
��������ƁA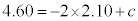 �C
�C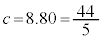 �C����āA�s�b�`z�̓X�g���C�hx��p���āA
�C����āA�s�b�`z�̓X�g���C�hx��p���āA �C�E�@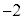 �@�G�I�@44 ......[��]�s�b�`��
�@�G�I�@44 ......[��]�s�b�`��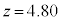 �̂Ƃ��A
�̂Ƃ��A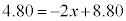 �C
�C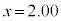
�J�@2�@�L�N�@00 ......[��]�X�g���C�hx�͈̔͂́A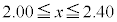 �ł��B
�ł��B �^�C�����ł��ǂ��Ȃ�̂�y���ő�̂Ƃ��ŁA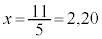 �̂Ƃ��Ay�̍ő�l��
�̂Ƃ��Ay�̍ő�l��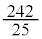 �ł��B
�ł��B
�P�@2�@�R�T�@20 ......[��]���̂Ƃ��̃s�b�`�́A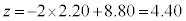
�V�@4�@�X�Z�@40 ......[��]���̂Ƃ��̃^�C���́B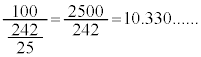 �C�l�̌ܓ�����10.33�\�@3 ......[��]
�C�l�̌ܓ�����10.33�\�@3 ......[��]
[2](1)  �́A��1���Y�Ƃ̔��Ђ��}�̔��̒��������Z���Ȃ�̂Ő������B
�́A��1���Y�Ƃ̔��Ђ��}�̔��̒��������Z���Ȃ�̂Ő������B  �́A1990�N�x�A2000�N�x�A2010�N�x�̑�1���Y�Ƃ́A�E���̕��������̂Ő������Ȃ��B
�́A1990�N�x�A2000�N�x�A2010�N�x�̑�1���Y�Ƃ́A�E���̕��������̂Ő������Ȃ��B
 �́A��2���Y�Ƃ̒����l�́A1990�N�x�ȍ~�A���Ɋ��̂Ő������B
�́A��2���Y�Ƃ̒����l�́A1990�N�x�ȍ~�A���Ɋ��̂Ő������B
 �́A��2���Y�Ƃ̑�1�l���ʐ��́A1985�N�x����1990�N�x�܂ʼnE�Ɋ��̂Ő������Ȃ��B
�́A��2���Y�Ƃ̑�1�l���ʐ��́A1985�N�x����1990�N�x�܂ʼnE�Ɋ��̂Ő������Ȃ��B
 �́A��3���Y�Ƃ̑�3�l���ʐ��́A����E�Ɋ��̂Ő������B
�́A��3���Y�Ƃ̑�3�l���ʐ��́A����E�Ɋ��̂Ő������B
 �́A��3���Y�Ƃ̍ŏ��l�́A����E�Ɋ��̂Ő������B
�́A��3���Y�Ƃ̍ŏ��l�́A����E�Ɋ��̂Ő������B
�^�@1�@�`�@3 ......[��](2) 1985�N�x�́A��1���Y�Ƃ�0�`26�͈̔͂ɂ����Ē����l��13�C��3���Y�Ƃ�45�`70�͈̔͂ɂ����Ē����l��54�C�����Ȃ��Ă���̂́A
�c�@1 ......[��]
1995�N�x�́A��1���Y�Ƃ�0�`17�͈̔͂ɂ����Ē����l��9�ő�1�l���ʐ���5�C��3���Y�Ƃ�51�`74�͈̔͂ɂ����Ē����l��58�ő�1�l���ʐ���55�C�����Ȃ��Ă���̂́A
�e�@4 ......[��]
(3) (I)�́A�}2�Ɛ}3�ŁA��1���Y�ƂƑ�2���Y�Ƃ̐}������ƁA1975�N�x�͕��̌X�����������ɉ����ĕ��сA2015�N�x�͂��ɎU���Ă���̂ŁA���B
(II)�́A��2���Y�ƂƑ�3���Y�Ƃ̐}������ƁA1975�N�x�͂��ɎU���Ă���̂ɁA2015�N�x�͌X�������̒����ɉ����ĕ���ł���̂ŁA�������B
(III)�́A��3���Y�ƂƑ�1���Y�Ƃ̐}������ƁA1975�N�x�͌X�������̒����ɉ����ĕ��сA2015�N�x�͂��ɎU���Ă���̂ŁA���B
�g�@5 ......[��]
(4) �}4������ƁA��1���Y�Ƃ̏A�ƎҊ�����2�`4%�̂Ƃ���Œj���̊������Ⴍ�A��1���Y�Ƃ̏A�ƎҊ�����6%�̂Ƃ���Œj���̊����������A��1���Y�Ƃ̏A�ƎҊ�����9%�`12%�̂Ƃ���Œj���̊����̍����_������B
�����̊����͋t�ɁA2�`4���̂Ƃ���ō����A6%�̂Ƃ���ŒႭ�A9%�`12%�̂Ƃ���ŒႢ�_������͂��ŁA�����Ȃ��Ă���̂́A
�i�@2 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 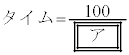 �@����@
�@����@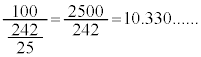 �C�l�̌ܓ�����10.33
�C�l�̌ܓ�����10.33