�@���ʃe�X�g���wIA '21�N��4��@
�~�����15�̓_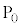 �C
�C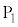 �C����C
�C����C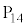 �������v���ɏ��ɕ���ł���B�ŏ��A�_
�������v���ɏ��ɕ���ł���B�ŏ��A�_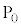 �ɐ�����B��������𓊂��ċ����̖ڂ��o������v����5��̓_�Ɉړ������A��̖ڂ��o��������v����3��̓_�Ɉړ�������B���̑�����J��Ԃ��B�Ⴆ�A���_
�ɐ�����B��������𓊂��ċ����̖ڂ��o������v����5��̓_�Ɉړ������A��̖ڂ��o��������v����3��̓_�Ɉړ�������B���̑�����J��Ԃ��B�Ⴆ�A���_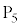 �ɂ���Ƃ��A��������𓊂���6�̖ڂ��o�����_
�ɂ���Ƃ��A��������𓊂���6�̖ڂ��o�����_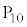 �Ɉړ�������B���ɁA5�̖ڂ��o����_
�Ɉړ�������B���ɁA5�̖ڂ��o����_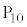 �ɂ����_
�ɂ����_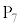 �Ɉړ�������B
�Ɉړ�������B (1) ���������5���āA�����̖ڂ� ��A��̖ڂ�
��A��̖ڂ� ��o��A�_
��o��A�_ �ɂ����_
�ɂ����_ �Ɉړ������邱�Ƃ��ł���B���̂Ƃ��A
�Ɉړ������邱�Ƃ��ł���B���̂Ƃ��A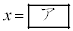 �C
�C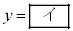 �́A�s�������
�́A�s�������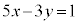 �̐������ɂȂ��Ă���B
�̐������ɂȂ��Ă���B (2) �s�������
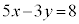 �@����@
�@����@�̂��ׂĂ̐�����x�Cy�́Ak�𐮐��Ƃ���
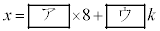 �C
�C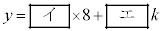
�ƕ\�����B�@�̐�����x�Cy�̒��ŁA�A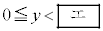 �������̂�
�������̂� 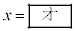 �C
�C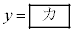
�ł���B���������āA���������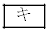 ���āA�����̖ڂ�
���āA�����̖ڂ� ��A��̖ڂ�
��A��̖ڂ� ��o��A�_
��o��A�_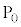 �ɂ����_
�ɂ����_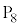 �Ɉړ������邱�Ƃ��ł���B
�Ɉړ������邱�Ƃ��ł���B (3) (2)�ɂ����āA���������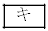 ���菭�Ȃ����������āA�_
���菭�Ȃ����������āA�_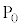 �ɂ����_
�ɂ����_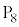 �Ɉړ������邱�Ƃ͂ł��Ȃ����낤���B
�Ɉړ������邱�Ƃ͂ł��Ȃ����낤���B (��)�@���v���܂��͎��v����15��̓_�Ɉړ�������ƌ��̓_�ɖ߂�B
(��)�ɒ��ӂ���ƁA�����̖ڂ� ��A��̖ڂ�
��A��̖ڂ� ��o��A��������𓊂����
��o��A��������𓊂���� ��ŁA�_
��ŁA�_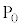 �ɂ����_
�ɂ����_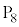 �Ɉړ������邱�Ƃ��ł���B���̂Ƃ��A
�Ɉړ������邱�Ƃ��ł���B���̂Ƃ��A �ł���B
�ł���B (4) �_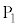 �C
�C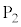 �C����C
�C����C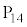 �̂�������_����I�сA�_
�̂�������_����I�сA�_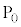 �ɂ��������������������Ă��̓_�Ɉړ�������B���̂��߂ɕK�v�ƂȂ�A��������𓊂���ŏ����l����B�Ⴆ�A���������1�������ē_
�ɂ��������������������Ă��̓_�Ɉړ�������B���̂��߂ɕK�v�ƂȂ�A��������𓊂���ŏ����l����B�Ⴆ�A���������1�������ē_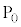 �ɂ����_
�ɂ����_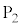 �ֈړ������邱�Ƃ͂ł��Ȃ����A���������2���ċ����̖ڂƊ�̖ڂ�1�o��A�_
�ֈړ������邱�Ƃ͂ł��Ȃ����A���������2���ċ����̖ڂƊ�̖ڂ�1�o��A�_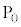 �ɂ����_
�ɂ����_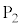 �ֈړ������邱�Ƃ��ł���B���������āA�_
�ֈړ������邱�Ƃ��ł���B���������āA�_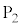 ��I�ꍇ�ɂ́A���̍ŏ���2��ł���B
��I�ꍇ�ɂ́A���̍ŏ���2��ł���B �_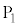 �C
�C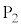 �C����C
�C����C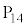 �̂����A���̍ŏ����ł��傫���͓̂_
�̂����A���̍ŏ����ł��傫���͓̂_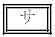 �ł���A���̍ŏ���
�ł���A���̍ŏ��� ��ł���B
��ł���B
 �̉Q
�̉Q  �@
�@ �@�@
�@�@ �@
�@ �@�@
�@�@ �@
�@ �@�@
�@�@ �@
�@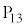 �@�@
�@�@ �@
�@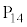
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� (4)�͖��_����点�Ȃ��悤�ɁA�Ƃ�����|�Ȃ̂����m��܂���B14�̓_�S���ɂ��āA�����v���A���v���ōŏ��ׂ�̂ł͂ƂĂ����Ԃ�����܂���B�ŏ���5��̓_�����邱�Ƃ�(3)�܂łł킩��̂ŁA�t��5��ȉ��łǂ̓_�ɍs���邩�ׂ邱�Ƃɂ��܂��B
(1) �s�������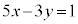 �̉��̈��
�̉��̈��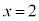 �C
�C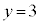 �ł��邱�Ƃ́A
�ł��邱�Ƃ́A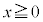 �Ȃ̂ŁA
�Ȃ̂ŁA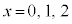 �Ɛ��l�����������ɂ킩��܂��B
�Ɛ��l�����������ɂ킩��܂��B �A�@2�@�C�@3 ......[��]
(2) 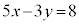 �@����@
�@����@ 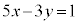 ��
��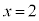 �C
�C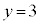 �����������A
�����������A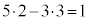 �̗��ӂ�8�������āA
�̗��ӂ�8�������āA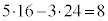 �@����A
�@����A�@�|�A���A
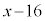 ��3�̔{���Ȃ̂ŁAk�𐮐��Ƃ��āA
��3�̔{���Ȃ̂ŁAk�𐮐��Ƃ��āA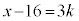 �Ƃ����܂��B���̂Ƃ��A
�Ƃ����܂��B���̂Ƃ��A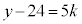 �C����āA
�C����āA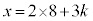 �C
�C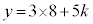 �@����B
�@����B�E�@3�@�G�@5 ......[��]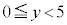 ���A
���A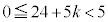 �C
�C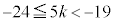 ���A
���A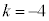
�B�ɑ�����āA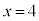 �C
�C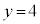
�I�@4�@�J�@4 ......[��]��������𓊂���́A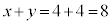
�L�@8 ......[��]���������8���āA�����̖ڂ�4��A��̖ڂ�4��o��ƁA ���甽���v����8�i���
���甽���v����8�i��� �ɗ��܂��B
�ɗ��܂��B (3)  ���玞�v����7�i�ނ�
���玞�v����7�i�ނ�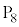 �ɗ��܂��B�����Ň@�̉E�ӂ�8��
�ɗ��܂��B�����Ň@�̉E�ӂ�8��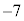 �ɂ����s����������l���܂��B
�ɂ����s����������l���܂��B 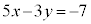 �@����C
�@����C
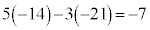 �@����D
�@����D�C�|�D���A
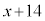 ��3�̔{���Ȃ̂ŁAl�𐮐��Ƃ��āA
��3�̔{���Ȃ̂ŁAl�𐮐��Ƃ��āA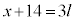 �Ƃ����܂��B���̂Ƃ��A
�Ƃ����܂��B���̂Ƃ��A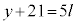 �C����āA
�C����āA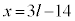 �C
�C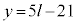
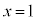 �C
�C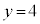
�����̖ڂ�1��A��̖ڂ�4��A���킹��5��������~��ƁA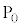 ���玞�v����7�i���
���玞�v����7�i���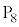 �ɗ��܂��B
�ɗ��܂��B
�N�@1�@�P�@4�@�R�@5 ......[��] (4) (2)�C(3)�Ɠ��l�ɁAm��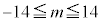 ���������Ƃ��āA
���������Ƃ��āA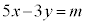 �Ƃ����s����������l����̂ł́A�ƂĂ����ԓ��ɂ�肫�邱�Ƃ͂ł��܂���B(3)��
�Ƃ����s����������l����̂ł́A�ƂĂ����ԓ��ɂ�肫�邱�Ƃ͂ł��܂���B(3)��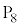 �ɍs���̂ł���ŏ���5�ɂȂ�̂ŁA���������U���5�ȉ��łǂ̓_�ɍs���邩�ׂ邱�Ƃɂ��܂��B
�ɍs���̂ł���ŏ���5�ɂȂ�̂ŁA���������U���5�ȉ��łǂ̓_�ɍs���邩�ׂ邱�Ƃɂ��܂��B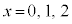 �Ƃ��āA
�Ƃ��āA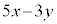 �̒l�ׂ�ƁA�ȉ��̕\�̂悤�ɂȂ�܂��B
�̒l�ׂ�ƁA�ȉ��̕\�̂悤�ɂȂ�܂��B | x | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 |
| y | 0 | 1 | 2 | 3 | 4 | 5 | 0 | 1 | 2 | 3 | 4 | 0 | 1 | 2 | 3 |
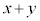 | 0 | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | 2 | 3 | 4 | 5 |
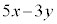 | 0 | 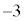 | 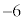 | 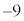 | 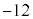 | 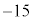 | 5 | 2 | 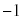 | 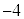 | 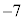 | 10 | 7 | 4 | 1 |
| �s�� | 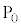 | 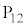 | 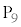 | 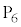 | 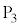 | 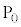 | 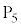 | 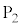 | 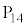 | 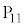 | 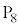 | 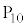 | 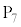 | 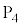 | 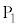 |
���̎��_��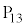 �����c��̂ŁA��������
�����c��̂ŁA�������� �Ƀ}�[�N���Ă��ǂ������m��܂��A�����ł͊m���߂ċN���܂��B
�Ƀ}�[�N���Ă��ǂ������m��܂��A�����ł͊m���߂ċN���܂��B
�s�������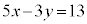 �@����E
�@����E
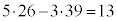 �@����F
�@����F�E�|�F���A
m�𐮐��Ƃ��āA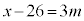 �Ƃ����ƁA
�Ƃ����ƁA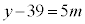 �C����āA
�C����āA 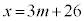 �C
�C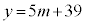
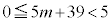 �Ƃ���ƁA
�Ƃ���ƁA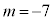 �C
�C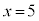 �C
�C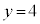 �C
�C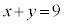
���������9��U���āA�����̖ڂ�5��A��̖ڂ�4��o��ƁA�����v����13�i���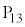 �ɗ��܂��B
�ɗ��܂��B
�s�������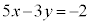 �@����G
�@����G
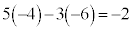 �@����H
�@����H�G�|�H���A
n�𐮐��Ƃ��āA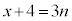 �Ƃ����ƁA
�Ƃ����ƁA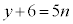 �C����āA
�C����āA 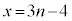 �C
�C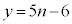
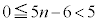 �Ƃ���ƁA
�Ƃ���ƁA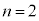 �C
�C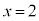 �C
�C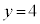 �C
�C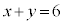
���������6��U���āA�����̖ڂ�2��A��̖ڂ�4��o��ƁA���v����2�i���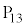 �ɗ��܂��B
�ɗ��܂��B
�ȏ���A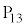 �ɗ��邽�߂ɂ��������U��ŏ���6�ł��B
�ɗ��邽�߂ɂ��������U��ŏ���6�ł��B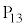 �ȊO�͍ŏ���5�ȉ��Ȃ̂ŁA�ŏ����ł��傫���̂�
�ȊO�͍ŏ���5�ȉ��Ȃ̂ŁA�ŏ����ł��傫���̂�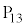 �ŁA���̍ŏ���6�T�@3�@�V�@6 ......[��]
�ŁA���̍ŏ���6�T�@3�@�V�@6 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B