内分・外分
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
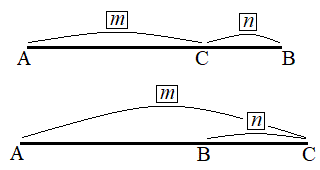 右上図において、線分AB上に点Cがあり、AC:CB = m:nであるとき、点CをABをm:nに内分する点と言います。
右上図において、線分AB上に点Cがあり、AC:CB = m:nであるとき、点CをABをm:nに内分する点と言います。
右下図において、直線AB上に点C (右下図では、線分ABのB側への延長上にCがあるように描かれています)があり、AC:CB = m:nであるとき、点CをABをm:nに外分する点と言います。右下図では、 です。
です。
 の場合には、ABをm:nに外分する点は、線分ABのA側への延長上にきます。
の場合には、ABをm:nに外分する点は、線分ABのA側への延長上にきます。
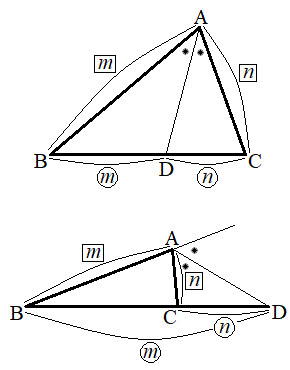
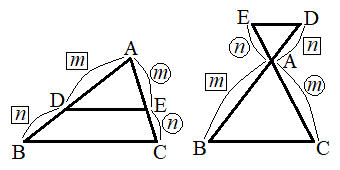 右の左図で、三角形ABCにおいて
右の左図で、三角形ABCにおいて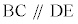 だとすると、AD:DB = AE:ECです。AD:DB = m:nであれば、点Dは線分ABをm:nに内分する点であり、点Eは線分ACをm:nに内分する点です。
だとすると、AD:DB = AE:ECです。AD:DB = m:nであれば、点Dは線分ABをm:nに内分する点であり、点Eは線分ACをm:nに内分する点です。
右の右図で、線分ABのA側の延長上に点D,線分ACのA側の延長上に点Eをとり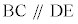 だとすると、AB:AD = AC:AEです。AB:AD = m:nであれば、点Aは、線分BDをm:nに内分する点であり、線分CEをm:nに内分する点です。
だとすると、AB:AD = AC:AEです。AB:AD = m:nであれば、点Aは、線分BDをm:nに内分する点であり、線分CEをm:nに内分する点です。
また、点Dは線分BAを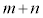 :nに外分する点で、点Eは線分CAを
:nに外分する点で、点Eは線分CAを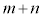 :nに外分する点です。
:nに外分する点です。
 定理:三角形ABCの
定理:三角形ABCの の二等分線は、辺BCを、AB:ACに内分する。
の二等分線は、辺BCを、AB:ACに内分する。
[証明] 頂点Cを通りDAに平行な直線と直線BAの交点をPとすると、 (錯角),
(錯角), (同位角)と
(同位角)と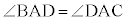 より
より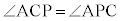 であり、三角形APCは二等辺三角形で、AC = AP,従って、
であり、三角形APCは二等辺三角形で、AC = AP,従って、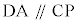 より、BD:DC = BA:AP = BA:AC (証明終)
より、BD:DC = BA:AP = BA:AC (証明終) この定理により、右上図でAB:AC = m:nとして、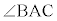 の二等分線と辺BCの交点Dは、辺BCをm:nに内分する点です。また、この定理の逆も成立します。
の二等分線と辺BCの交点Dは、辺BCをm:nに内分する点です。また、この定理の逆も成立します。
定理: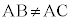 である三角形ABCの
である三角形ABCの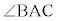 の外角の二等分線は、辺BCを、AB:ACに外分する。
の外角の二等分線は、辺BCを、AB:ACに外分する。
[証明] 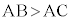 とします。線分BAのA側への延長上に点Xをとる。頂点Cを通りDAに平行な直線と辺BAの交点をPとすると、
とします。線分BAのA側への延長上に点Xをとる。頂点Cを通りDAに平行な直線と辺BAの交点をPとすると、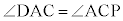 (錯角),
(錯角),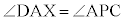 (同位角)と
(同位角)と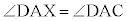 より
より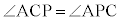 であり、三角形APCは二等辺三角形で、AC = AP,従って、
であり、三角形APCは二等辺三角形で、AC = AP,従って、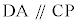 より、BD:DC = BA:AP = BA:AC (証明終)
より、BD:DC = BA:AP = BA:AC (証明終) この定理により、右下図でAB:AC = m:nとして、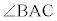 の外角の二等分線と直線BCの交点Dは、辺BCをm:nに外分する点です。また、この定理の逆も成立します。
の外角の二等分線と直線BCの交点Dは、辺BCをm:nに外分する点です。また、この定理の逆も成立します。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。