�������E�s�����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�����F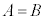 �Ƃ����`�̎��B�C�R�[��'='�̍���A�������A�C�R�[��'='�̉E�����E���ƌ����B
�Ƃ����`�̎��B�C�R�[��'='�̍���A�������A�C�R�[��'='�̉E�����E���ƌ����B
�������F�����ŕ\���ꂽ�ϐ����ǂ������l���Ƃ�ׂ��Ȃ̂������߂Ă��铙���B��������������̒l�����ƌ����B
�P�����F�����ɁA����������������Ȃ�l�������Ă����藧�����B
�s�����F���ʂ̑召�W��s������p���ĕ\�������B�����Ɠ��l�ɁA�s�����̍��������ӁA�E�����E�ӂƌ����B
�s�����̈Ӗ��F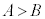 ���hA��B�����傫���h�Ƃ����Ӗ��BA��B�́A�hA��B�Ɠ�������B���傫���h�Ƃ����Ӗ��B
���hA��B�����傫���h�Ƃ����Ӗ��BA��B�́A�hA��B�Ɠ�������B���傫���h�Ƃ����Ӗ��B
�����̐����F���Ƃ��ƁA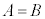 �Ƃ����������������ꍇ�A
�Ƃ����������������ꍇ�A
(1) ���ӂɓ�����C�������Ă����������藧�B�܂�A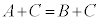
(2) ���ӂ��瓯����C�������Ă����������藧�B�܂�A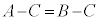
(3) ���ӂɓ�����C�������Ă����������藧�B�܂�A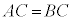
(4) ���ӂ�0�ȊO�̓�����C�Ŋ����Ă����������藧�B�܂�A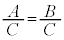
�s�����̐����F���Ƃ��ƁA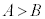 �Ƃ����s�������������ꍇ(
�Ƃ����s�������������ꍇ(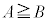 �ł�����)�A
�ł�����)�A
(1) ���ӂɓ�����C�������Ă��s�����͕ς��Ȃ��B�܂�A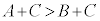
(2) ���ӂ��瓯����C�������Ă��s�����͕ς��Ȃ��B�܂�A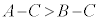
(3) ���ӂɓ�������C�������Ă��s�����͕ς��Ȃ��B�܂�A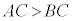
�@���ӂɓ�������C��������ƕs�����̌������t�ɂȂ�B�܂�A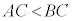
(4) ���ӂ�����C�Ŋ����Ă��s�����͕ς��Ȃ��B�܂�A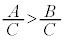
�@���ӂ�����C�Ŋ���ƕs�����̌������t�ɂȂ�B�܂�A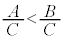
(5) ����ɁA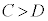 �Ƃ����s����������ꍇ�A
�Ƃ����s����������ꍇ�A
�E�傫�����̓��m�������킹�����̂͏��������̓��m���������̂����傫���B�܂�A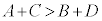
�EA�CB�CC�CD���S�Đ����Ȃ�A�傫�����̓��m���������̂͏��������̓��m���������̂����傫���B�܂�A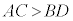
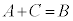 �Ƃ����`�̎�������ꍇ�A�����̐���(2)�ɂ��A���ӂ���C�������Ă����������藧�̂ŁA
�Ƃ����`�̎�������ꍇ�A�����̐���(2)�ɂ��A���ӂ���C�������Ă����������藧�̂ŁA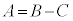 �����藧���܂��B
�����藧���܂��B
���ӂɂ���C���E�ӂɉ���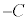 �ɂȂ邱�Ƃɒ��ӂ��Ă��������B���̎��ό`�̂��Ƃ��A�hC���ڍ������h�ƌ����܂��B
�ɂȂ邱�Ƃɒ��ӂ��Ă��������B���̎��ό`�̂��Ƃ��A�hC���ڍ������h�ƌ����܂��B
1���������F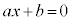 (
(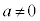 )
)
b���ڍ�����ƁA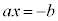
���́A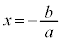
1���s�����F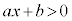 (
(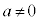 )
)
b���ڍ�����ƁA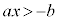
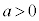 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A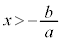
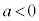 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A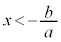
��1�D(1) 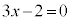 �̉��́A
�̉��́A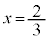
(2) 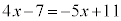
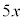 �����ӂɁA7���E�ӂɈڍ����āA
�����ӂɁA7���E�ӂɈڍ����āA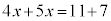
�� 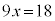
���́A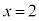
(3) 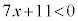 �̉��́A
�̉��́A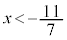
(4) 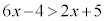
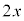 �����ӂɁA4���E�ӂɈڍ����āA
�����ӂɁA4���E�ӂɈڍ����āA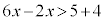
�� 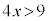
���́A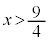
(5) 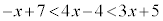
���̕s������������ƁA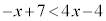
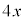 �����ӂɁA7���E�ӂɈڍ�����ƁA
�����ӂɁA7���E�ӂɈڍ�����ƁA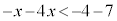
�� 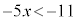
�� 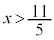 (�s�����̌����ɒ���) ����@
(�s�����̌����ɒ���) ����@
�^�s�����̉E�̕s������������ƁA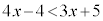
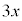 �����ӂɁA4���E�ӂɈڍ�����ƁA
�����ӂɁA4���E�ӂɈڍ�����ƁA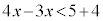
�� 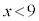 ����A
����A
�^�s������2�s�������������Ƃ������Ƃ́A�@�ƇA�Ɨ�������������Ȃ�������Ȃ�(�g�@���A�h�ƌ���)�̂ŁA
���́A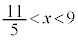
��2�D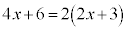
���̎��́Ax�ɂǂ�Ȏ��������Ă��������܂��B���̂悤�Ȏ����P�����ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B