関数


【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
 【広告】広告はここまでです。
2つの実数x，yがあって、xの値が決まるとそれに対応して?yの値がだた1つ決まるとき、yをxの関数と言う。
yがxの関数であることを、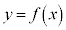のように表す。
xが取り得る値の範囲を関数の定義域、yがとりうる値の範囲を関数の値域を言う。
x，yは、実数という制約をつけないこともあります。整数x，ベクトル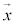の関数ということもあります。数学を離れると、文字列、とか、時刻・日付、というようなこともあります。高校の範囲外ですが、複素数に対する関数を考えることもあり、複素関数と呼ばれます。また、yが2通り以上の値をとる多値関数というようなものもあります。2つ以上の数値に対して1つのyの値が定まる多変数関数と呼ばれる関数もあります。

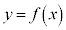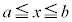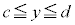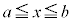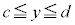関数：において、のとき、なら、定義域は，値域はです。
xが実数全体をとりうるときには、定義域は実数全体で、”実数全体で定義された関数”というような言い方をします。

関数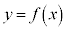：について、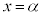における関数の値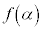は、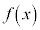をxで表した式のxに、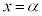を代入して計算します。

例1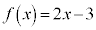．の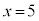における関数の値は、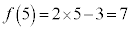です。

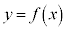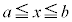関数：において、のとき、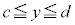だとして、定義域内の実数α，β (つまり、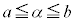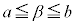，)に対して、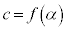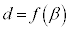，であれば、cを最小値、dを最大値と言う。

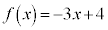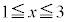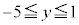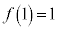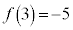例2．のにおける最大値、最小値は、であって、，より、
最大値：1，最小値：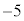

定義域が、片端、あるいは、両端を含まないような範囲の場合、つまり、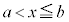とか、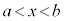などのような場合、最大値、最小値が存在しない場合があります。

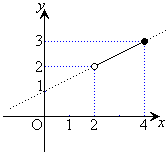関数のグラフを、片端、あるいは、両端を含まないような範囲で考える場合、端点を含んでいないことを明示するために、例えば、1次関数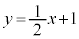：を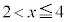の範囲で考える場合には、右図のように、端点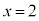に白丸、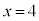に黒丸をつけておきます。白丸を含まず、黒丸を含まないので、この関数には、最小値は存在せず、最大値は3です。


【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
 【広告】広告はここまでです。
　　数学基礎事項TOP　　数学TOP　　TOPページに戻る

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。
©2005-2024
(有)りるらる
苦学楽学塾 随時入会受付中！
理系大学受験ネット塾苦学楽学塾
(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。