���k�嗝�n���w'08�N�O��[1]
������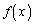 �ɂ��āA���̏���(i)�C(ii)�C(iii)���l����B
�ɂ��āA���̏���(i)�C(ii)�C(iii)���l����B
���̂Ƃ��A�ȉ��̖₢�ɓ�����B
(1) ����(i)���݂���������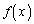 �̎�����4�ȉ��ł��邱�Ƃ������B
�̎�����4�ȉ��ł��邱�Ƃ������B
(2) ����(i)�C(ii)�C(iii)�����ׂĂ݂��������� �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�������Ƃ����̂́A�������������킹���葫�����킹���肵�Ăł��鎮�ł����āA�u�����v�͕������������Ă��邩�A�Ƃ������A�܂�A0�ȏ�̐����ɂȂ�܂��B�P�Ɂg������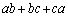 �h�ƌ����ꍇ�́A�e���ŕ�����2�����Ă���̂ŁA2���̑������ł����A�g
�h�ƌ����ꍇ�́A�e���ŕ�����2�����Ă���̂ŁA2���̑������ł����A�g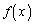 �h�ƌ����ꍇ�́Ax�ɒ��ڂ��Ă���̂ŁA
�h�ƌ����ꍇ�́Ax�ɒ��ڂ��Ă���̂ŁA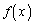 �̒���
�̒��� �Ƃ�����������Ƃ��ɂ́A�������Ă���x�̌���4�������Ƃ��܂��B
�Ƃ�����������Ƃ��ɂ́A�������Ă���x�̌���4�������Ƃ��܂��B
(1) n��0�ȏ�̐����Ƃ��A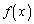 �̒���n���̍��������āA
�̒���n���̍��������āA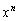 ���܂܂��Ƃ��܂��B����
���܂܂��Ƃ��܂��B����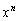 ��x��
��x��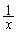 ��������ƁA
��������ƁA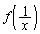 �̒���
�̒���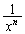 ���o�Ă��܂��B�܂��A
���o�Ă��܂��B�܂��A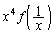 �ɂ�
�ɂ� �Ƃ��������o�Ă��܂��B
�Ƃ��������o�Ă��܂��B  ��x�̑������ł��邽�߂ɂ́A
��x�̑������ł��邽�߂ɂ́A ���̊e����x�̎w����0�ȏ�̐����łȂ���Ȃ�܂���B
���̊e����x�̎w����0�ȏ�̐����łȂ���Ȃ�܂���B
�� 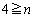 �����A
�����A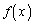 �ɂ�4���܂ł̍������܂܂�Ȃ��̂ŁA
�ɂ�4���܂ł̍������܂܂�Ȃ��̂ŁA �̎�����4�ȉ��ł��B
�̎�����4�ȉ��ł��B
(2) (1)���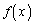 ��4���̑������Ȃ̂ŁA
��4���̑������Ȃ̂ŁA �Ƃ����܂��B
����(i)���A
���ꂪ�P�����ƂȂ邽�߂ɁA
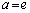 �C
�C �@����@
�@����@����ƁA����(iii)���A
��  �@����A
�@����A
����(ii)�ɂ����āA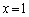 �Ƃ���ƁA
�Ƃ���ƁA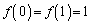
�@���A �@����B
�@����B
�A�ɑ�����āA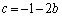 �@����C
�@����C
����(ii)�ɂ����āA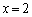 �Ƃ���ƁA
�Ƃ���ƁA
�@�C�B�C�C���A �� 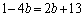 ��
�� 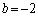 �C���A
�C���A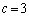
�@���A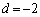
�����ƇB���A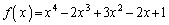 �@����D
�@����D
����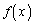 �́A
�́A ���A����(ii)���݂����܂��B
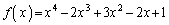 ......[��]
......[��]
�NjL�D��L�̇D�� �͋��܂�̂ł����A�����ő��A�u�����v�Ƃ���Ă͂����܂���B
�͋��܂�̂ł����A�����ő��A�u�����v�Ƃ���Ă͂����܂���B
��L�ł́A����(i)�ɂ��Ă͂��ׂĂ�x�C(iii)�ɂ��Ă�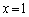 �̏ꍇ�ɂ��Ċm�F�ł��Ă��܂����A����(ii)�́A�����ł͂���܂���Bb�����߂邽�߂ɁA����(ii)�ɂ����āA
�̏ꍇ�ɂ��Ċm�F�ł��Ă��܂����A����(ii)�́A�����ł͂���܂���Bb�����߂邽�߂ɁA����(ii)�ɂ����āA �C
�C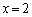 �Ƃ��Ă݂������ŁA����x�̒l�ɂ��āA�{����
�Ƃ��Ă݂������ŁA����x�̒l�ɂ��āA�{����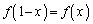 �����������̂��A�m�F����Ă��Ȃ��̂ł��B
�����������̂��A�m�F����Ă��Ȃ��̂ł��B
����������ƁA����(ii)���݂������߂̕K�v�������g �h�ƂȂ���(����(ii)�ˁg
�h�ƂȂ���(����(ii)�ˁg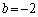 �h)�����ł����āA�g
�h)�����ł����āA�g �h������(ii)�̂��߂̏\�������ł��邱��(�g
�h������(ii)�̂��߂̏\�������ł��邱��(�g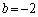 �h�ˏ���(ii))���m�F����Ă��܂���B�����ŁA�D�ȉ��Ŏ��ۂ�
�h�ˏ���(ii))���m�F����Ă��܂���B�����ŁA�D�ȉ��Ŏ��ۂ� ���v�Z���Ċm�F����K�v������܂����B
���v�Z���Ċm�F����K�v������܂����B
�K�v���A�\�����́A�Z���^�[�����̕p�o�e�[�}�ł����A����s�\���Ȃ��߂ɁA�Z���^�[�������ʼn��M��|���ĉ����A�Ƃ����b���悭�����܂��B
�u�K�v�����v�Ƃ����̂́A�v���������߂ɍŒ���K�v�ȏ���(��邢����)�ł���A�u�\�������v�Ƃ����̂́A����ł���Ηv���͊��S�ɖ��������Ƃ�������(����������)�ł��B
�u�K�v�����v�����߂������ł́A����ꂽ�����S�������ɓK���Ă��邩�������A�u�\�������v�����߂������ł́A����ꂽ���͊m���ɏ������������ɂ��������邩���m��Ȃ��A�Ǝv���悤�ɂ��܂��傤�B�u�K�v�\�������v�����߂�A�Ƃ������Ƃ́A�����̓��͂��ׂėv�������Ă��āA���ɂ͓��͂Ȃ��A�Ƃ��������߂�A�Ƃ������Ƃł��B
�u�K�v�����v�A�u�\�������v�Ƃ������t�̈Ӗ����������藝�����Ă����܂��傤�B�Ȃ��A�����E�������Q�Ƃ��Ă��������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B