���k�嗝�n���w'10�N���[1]
n��2�ȏ�̎��R���Ƃ���B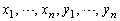 ��
��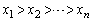 �C
�C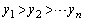 ���������Ƃ���B
���������Ƃ���B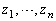 ��
��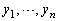 ��C�ӂɕ��בւ������̂Ƃ���Ƃ��A
��C�ӂɕ��בւ������̂Ƃ���Ƃ��A
�����藧���Ƃ������B�܂��A���������藧�̂͂ǂ̂悤�ȂƂ���������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���w�I�A�[�@�Ɏ������ޕ����Ɉ�H�v�K�v�Ȗ��ł��B�Ȃ��A'87�N���嗝�n[5]�ŁA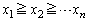 �C
�C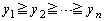 �Ƃ���
�Ƃ���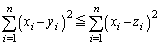 ���ؖ������肪�o�肳��Ă��܂��B
���ؖ������肪�o�肳��Ă��܂��B
(�T) 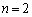 �̂Ƃ��A
�̂Ƃ��A (ii) 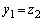 �C
�C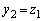 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A (i)�C(ii)���A
�^�s�����͐��藧���A���������́A(i)���A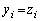 (
(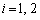 )�̂Ƃ��ł��B
)�̂Ƃ��ł��B (�U) 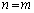 �̂Ƃ��A�^�s���������藧�Ɖ��肵�܂��B�܂�A
�̂Ƃ��A�^�s���������藧�Ɖ��肵�܂��B�܂�A 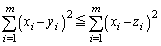 �@����@
�@����@�����藧���A�܂��A���������́A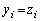 (
(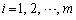 )�̂Ƃ��A�Ɖ��肵�܂��B
)�̂Ƃ��A�Ɖ��肵�܂��B (i) 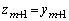 �̂Ƃ��A
�̂Ƃ��A �@�̗��ӂɁA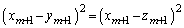 �������邱�Ƃɂ��A
�������邱�Ƃɂ��A 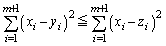 �@����A
�@����A�����藧���A���������́A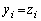 (
(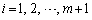 )�̂Ƃ��ł��B
)�̂Ƃ��ł��B (ii) �@��m������Ȃ鐔��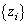 �ɂ�����
�ɂ�����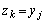 �ł��������̂��A�V����
�ł��������̂��A�V����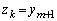 �C
�C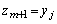 (j�Ck�́A
(j�Ck�́A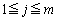 �C
�C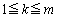 �C
�C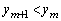 ��������)�Ƃ��ē�����A
��������)�Ƃ��ē�����A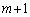 �����琬�鐔��
�����琬�鐔��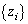 ���l���܂��B����ŁA
���l���܂��B����ŁA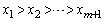 �C
�C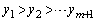 �C
�C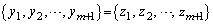 �ƂȂ�C�ӂ̐���
�ƂȂ�C�ӂ̐���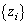 ���\�����邱�Ƃ��ł��܂��B
���\�����邱�Ƃ��ł��܂��B 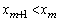 �Ƃ��āA�@�̗��ӂɁA
�Ƃ��āA�@�̗��ӂɁA��������ƁA�E�ӂ́A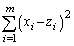 �̑�k���ڂ�����
�̑�k���ڂ�����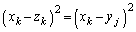 ����A�V���Ȑ���
����A�V���Ȑ���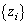 �̍����g���Ăł���
�̍����g���Ăł���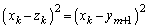 �ɓ���ւ��A�����
�ɓ���ւ��A�����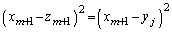 ��t�����邱�ƂɂȂ�̂ŁA
��t�����邱�ƂɂȂ�̂ŁA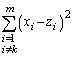 ��
��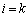 �ƂȂ鍀���������a���Ƃ��āA
�ƂȂ鍀���������a���Ƃ��āA 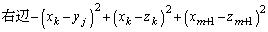
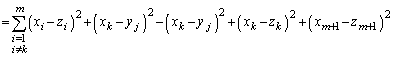
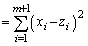 �@����B�@(�@�̐���
�@����B�@(�@�̐���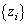 �ƇB�̐���
�ƇB�̐���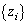 �͑�k���ڂ��قȂ邱�Ƃɒ��ӂ��Ă�������)
�͑�k���ڂ��قȂ邱�Ƃɒ��ӂ��Ă�������)�ȏ���A
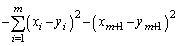 �@����C
�@����C�����ŁA����ɂ��A
�C�̎c��̕����́A
����āA�C���A
(i)�C(ii)���A
�����藧���A���������́A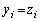 (
(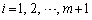 )�̂Ƃ��ł��B
)�̂Ƃ��ł��B
����āA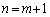 �̂Ƃ��ɂ��^�s�����͐������܂��B
�̂Ƃ��ɂ��^�s�����͐������܂��B (�T)�C(�U)���A2�ȏ�̎��R���ɑ��āA
�����藧���܂��B�܂��A�����́A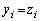 (
(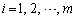 ) ......[��]�@�̂Ƃ��ɐ������܂��B
) ......[��]�@�̂Ƃ��ɐ������܂��B
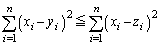 ��
�� 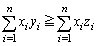 �@����D
�@����D�ł��B
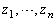 ��
��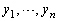 ��C�ӂɕ��בւ������̂Ƃ���Ƃ��A
��C�ӂɕ��בւ������̂Ƃ���Ƃ��A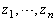 ��2���I��ő傫�����ɂȂ�悤�ɕ��בւ��Ă����ƁA�L����(���X
��2���I��ő傫�����ɂȂ�悤�ɕ��בւ��Ă����ƁA�L����(���X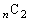 ��)�̕��בւ���
��)�̕��בւ���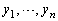 �ɂȂ�܂��B
�ɂȂ�܂��B
�����ŁA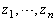 �̂�����2��
�̂�����2��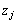 �C
�C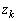 (j�Ck�́A
(j�Ck�́A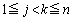 ��������)��I��ŁA
��������)��I��ŁA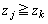 �ł���A
�ł���A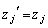 �C
�C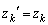 �C
�C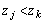 �ł���A
�ł���A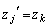 �C
�C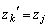 �C����
�C����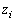 (i�́A
(i�́A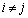 �C
�C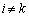 �C
�C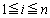 ��������)�ɂ��ẮA
��������)�ɂ��ẮA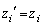 �ƂȂ�悤�ɂ��āA�V����
�ƂȂ�悤�ɂ��āA�V����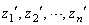 �����ƁA
�����ƁA �ƂȂ邱�Ƃ���A�D�������܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 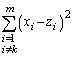 ��
��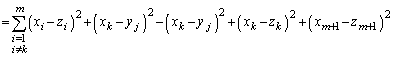
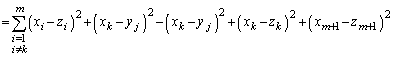
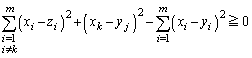 �@(
�@(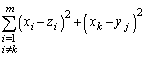 �͇@��
�͇@��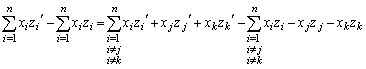
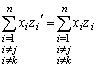 )
)