高次の導関数 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
nを3以上の自然数として、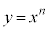 の導関数を考えます。
の導関数を考えます。
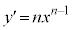
です。この右辺の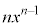 の導関数を求めると、
の導関数を求めると、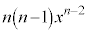 となりますが、左辺の
となりますが、左辺の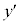 の導関数は、yから2回微分されることになるので、もう一つ、プライム記号をつけて、
の導関数は、yから2回微分されることになるので、もう一つ、プライム記号をつけて、
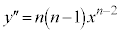
と表すことにします。さらに、微分して、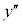 の導関数は、yから3回微分されることになるので、プライム記号を3つつけて表し、
の導関数は、yから3回微分されることになるので、プライム記号を3つつけて表し、
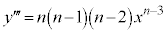
となります。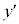 を第1次(第1階)の導関数、
を第1次(第1階)の導関数、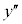 を第2次(第2階)の導関数、
を第2次(第2階)の導関数、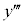 を第3次(第3階)の導関数と呼びます。
を第3次(第3階)の導関数と呼びます。
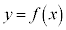 と書くとき、
と書くとき、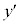 を
を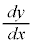 ,
,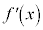 ,
,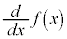 とも書きますが、
とも書きますが、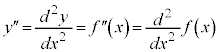 ,
,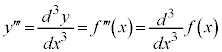 です。
です。
4次以上になると、プライム記号の数が多くなるので、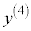 と書いて第4次(第4階)の導関数ということにします。
と書いて第4次(第4階)の導関数ということにします。
n回微分すると、
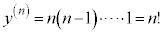
となります。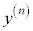 を第n次(第n階)の導関数と言います。
を第n次(第n階)の導関数と言います。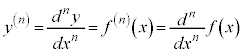 (
(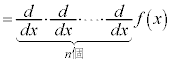 )です。
)です。
以下、m,nを自然数として、
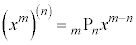
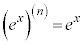 (底がeの指数関数は何回微分しても指数関数のまま)
(底がeの指数関数は何回微分しても指数関数のまま)
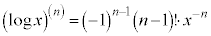 (
(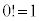 とします)
とします)
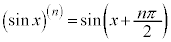
などが言えます。
例.(1) 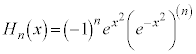 (
(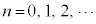 )として求められる多項式をエルミート多項式と言います。
)として求められる多項式をエルミート多項式と言います。
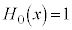 ,
,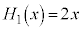 ,
,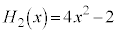 ,
,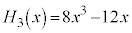 ,・・・
,・・・
などとなっています。
(2) 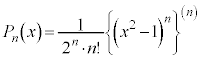 (
(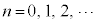 )として求められる多項式をルジャンドル多項式と言います。
)として求められる多項式をルジャンドル多項式と言います。
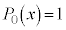 ,
,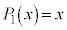 ,
,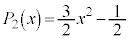 ,
,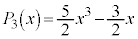 ,・・・
,・・・
などとなっています。
(1),(2)とも物理学で登場する重要な多項式です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 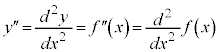 ,
,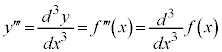 です。
です。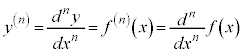 (
(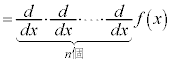 )です。
)です。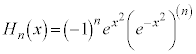 (
(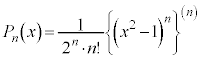 (
(