�P�����̏���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
(1)  ���A�C�ӂ̎���x�Cy�ɂ��Đ������� ��
���A�C�ӂ̎���x�Cy�ɂ��Đ������� �� 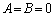
(2) 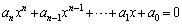 ���C�ӂ̎���x�ɂ��Đ�������
���C�ӂ̎���x�ɂ��Đ�������
�@�� 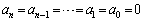
(3) 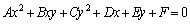 ���A�C�ӂ̎���x�Cy�ɂ��Đ������� ��
���A�C�ӂ̎���x�Cy�ɂ��Đ������� �� 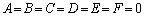
[�ؖ�](1) 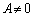 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA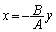 �ƂȂ�y��1�̒l�ɑ���x�̒l��1�Ɋm�肵�Ă��܂��܂��B
�ƂȂ�y��1�̒l�ɑ���x�̒l��1�Ɋm�肵�Ă��܂��܂��B
����ł́A�C�ӂ̎���x�Cy�ɂ��� ����������Ƃ��������ɔ����܂��B
����������Ƃ��������ɔ����܂��B
�� 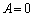 �C
�C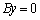
y��0�ȊO�̒l����蓾��̂ŁA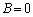 �C����āA
�C����āA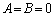
�t�ɁA �̂Ƃ��A���炩�ɁA�C�ӂ̎���x�Cy�ɂ��āA
�̂Ƃ��A���炩�ɁA�C�ӂ̎���x�Cy�ɂ��āA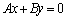 ���������܂��B�@(�ؖ��I)
���������܂��B�@(�ؖ��I)
(2) 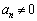 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA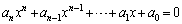 ����@ ���C�ӂ̎���x�ɂ��Đ������邩��A���قȂ�
����@ ���C�ӂ̎���x�ɂ��Đ������邩��A���قȂ�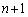 �̎���
�̎��� �ɂ��ć@���������܂��B����́An���������@�̑��قȂ�������Xn�ł���Ƃ��������ɔ����܂��B
�ɂ��ć@���������܂��B����́An���������@�̑��قȂ�������Xn�ł���Ƃ��������ɔ����܂��B
�� 
�ȉ��A���l�ɂ��āA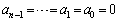
�t�ɁA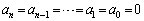 �̂Ƃ��A���炩�ɁA�C�ӂ̎���x�ɂ��āA
�̂Ƃ��A���炩�ɁA�C�ӂ̎���x�ɂ��āA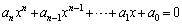 ���������܂��B�@(�ؖ��I)
���������܂��B�@(�ؖ��I)
(3)  ��x�ɂ��Đ�������ƁA
��x�ɂ��Đ�������ƁA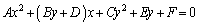
���̓������C�ӂ̎���x�ɂ��Đ������邩��A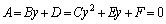
���ł��C�ӂ̎���y�ɂ��Đ������邩��A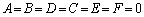
�t�ɁA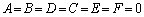 �̂Ƃ��A���炩�ɁA�C�ӂ̎���x�Cy�ɂ��āA
�̂Ƃ��A���炩�ɁA�C�ӂ̎���x�Cy�ɂ��āA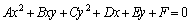 ���������܂��B�@(�ؖ��I)
���������܂��B�@(�ؖ��I)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B