不定積分 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
微分可能な関数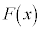 があって、
があって、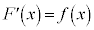 となるとき、つまり、
となるとき、つまり、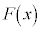 の導関数が
の導関数が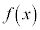 となるとき、
となるとき、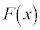 を
を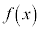 の原始関数と言う。
の原始関数と言う。
このとき、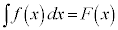 と書くことにする。記号
と書くことにする。記号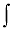 はインテグラル(integral)と読む。
はインテグラル(integral)と読む。
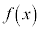 の原始関数は一つに定まらない。
の原始関数は一つに定まらない。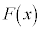 が
が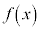 の原始関数であるなら、Cを定数として、
の原始関数であるなら、Cを定数として、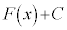 も
も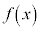 の原始関数である。
の原始関数である。
なぜなら、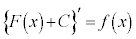 ,つまり、
,つまり、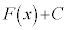 の導関数も
の導関数も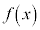 となるからである。
となるからである。
その意味で、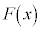 を
を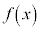 の原始関数のうちの一つだとして、
の原始関数のうちの一つだとして、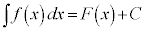 と書き、Cを積分定数と言い、
と書き、Cを積分定数と言い、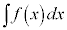 を
を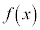 の不定積分と言う。
の不定積分と言う。
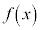 から不定積分
から不定積分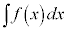 を求めることを、
を求めることを、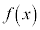 を積分すると言う。
を積分すると言う。
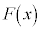 から導関数
から導関数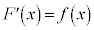 を求めることを微分すると言うが、これの逆演算、
を求めることを微分すると言うが、これの逆演算、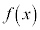 から原始関数
から原始関数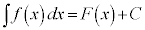 (C:積分定数)を求めることを積分すると言うので、微分と積分は逆の関係にある。
(C:積分定数)を求めることを積分すると言うので、微分と積分は逆の関係にある。
注1.正確には、aを定数、xを変数として、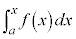 を不定積分と言います。大学入試の範囲では気にする必要はありません。原始関数が存在しないのに不定積分が存在する例が知られていますが、大学入試の範囲では、原始関数と不定積分は同じ意味だと考えて大丈夫です。
を不定積分と言います。大学入試の範囲では気にする必要はありません。原始関数が存在しないのに不定積分が存在する例が知られていますが、大学入試の範囲では、原始関数と不定積分は同じ意味だと考えて大丈夫です。
注2.不定積分の結果には必ず、積分定数Cをつけてください。つけなければ不十分解になります。
注3.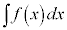 の
の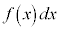 は、
は、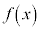 と
と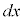 の積だと考えてください(詳しくは、区分求積法を参照)。
の積だと考えてください(詳しくは、区分求積法を参照)。
積分は微分の逆演算と言えるので、微分の公式から積分の公式を作ることができます。
cを実数の定数だとして、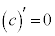
∴ 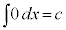
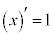
∴ 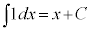 (C:積分定数)
(C:積分定数)
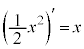
∴ 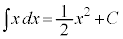 (C:積分定数)
(C:積分定数)
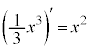
∴ 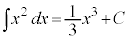 (C:積分定数)
(C:積分定数)
一般に、nを0以上の整数だとして、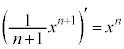
∴ 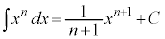 (C:積分定数) (C:積分定数) |
また、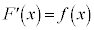 ,
,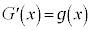 ,a,bを定数だとして、
,a,bを定数だとして、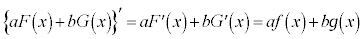
よって、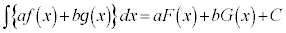 (C:積分定数)
(C:積分定数)
従って、不定積分の計算を以下のようにして行うことができます。
例1.a,b,cを定数だとして、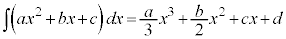 (d:積分定数)
(d:積分定数)
ちなみに、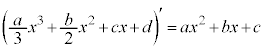 です。
です。
注.一般に、a,b,c,dを定数として、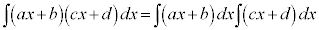 は成り立ちません。この場合には、次のように展開してから積分することになります。
は成り立ちません。この場合には、次のように展開してから積分することになります。
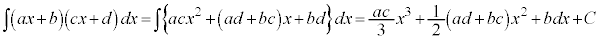 (C:積分定数)
(C:積分定数)
例2.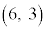 を通過する曲線:
を通過する曲線: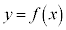 の
の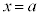 における接線の傾きが
における接線の傾きが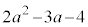 のとき、関数
のとき、関数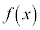 を求める。
を求める。
[解答] 与えられた条件より、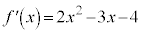
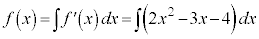
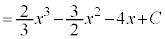 (C:積分定数)
(C:積分定数)
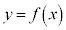 は
は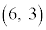 を通過するので、
を通過するので、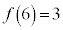
∴ 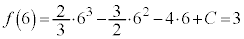
∴ 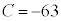
∴ 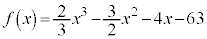 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。