�s�����̕\���̈��@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
(1) ���W���ʏ�ŁA �̕\���̈�́A�����F
�̕\���̈�́A�����F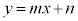 ���㑤�̕���
���㑤�̕���
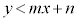 �̕\���̈�́A�����F
�̕\���̈�́A�����F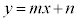 ��艺���̕���
��艺���̕���
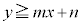 �̕\���̈�́A�����F
�̕\���̈�́A�����F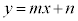 ����㑤�̕���(������̓_���܂�)
����㑤�̕���(������̓_���܂�)
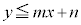 �̕\���̈�́A�����F
�̕\���̈�́A�����F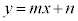 ���牺���̕���(������̓_���܂�)
���牺���̕���(������̓_���܂�)
(2) ���W���ʏ�ŁA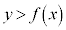 �̕\���̈�́A�Ȑ��F
�̕\���̈�́A�Ȑ��F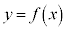 ���㑤�̕���
���㑤�̕���
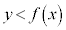 �̕\���̈�́A�Ȑ��F
�̕\���̈�́A�Ȑ��F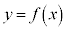 ��艺���̕���
��艺���̕���
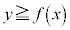 �̕\���̈�́A�Ȑ��F
�̕\���̈�́A�Ȑ��F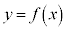 ����㑤�̕���(�Ȑ���̓_���܂�)
����㑤�̕���(�Ȑ���̓_���܂�)
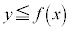 �̕\���̈�́A�Ȑ��F
�̕\���̈�́A�Ȑ��F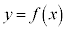 ���牺���̕���(�Ȑ���̓_���܂�)
���牺���̕���(�Ȑ���̓_���܂�)
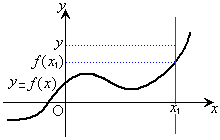 (2)�ŁA
(2)�ŁA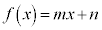 �Ƃ������̂�(1)�Ȃ̂ŁA(2)���l���܂��B
�Ƃ������̂�(1)�Ȃ̂ŁA(2)���l���܂��B
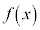 �̒�`��ɑ�����x�̒l��1�����Ă���
�̒�`��ɑ�����x�̒l��1�����Ă���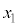 �Ƃ��܂��B
�Ƃ��܂��B
x���ɐ����Ȓ����F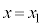 ��ɂ����āA
��ɂ����āA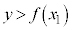 �����̂́A�_
�����̂́A�_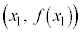 �����㑤�̕����ł��B
�����㑤�̕����ł��B
�t�ɁA�����F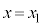 ��ɂ����āA
��ɂ����āA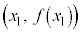 �����㑤�ɂ���_
�����㑤�ɂ���_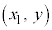 �́A
�́A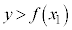 �����܂��B
�����܂��B
�]���āA���W���ʏ�ŁA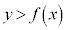 �̕\���̈�́A�Ȑ��F
�̕\���̈�́A�Ȑ��F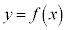 ���㑤�̕���(�Ȑ��F
���㑤�̕���(�Ȑ��F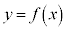 ��͊܂݂܂���)�ł��B
��͊܂݂܂���)�ł��B
���l�ɁA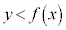 �̕\���̈�́A�Ȑ��F
�̕\���̈�́A�Ȑ��F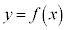 ��艺���̕����ɂȂ�܂��B
��艺���̕����ɂȂ�܂��B
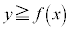 �̕\���̈�́A�Ȑ��F
�̕\���̈�́A�Ȑ��F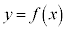 ��̓_���܂ނ̂ŁA�Ȑ��F
��̓_���܂ނ̂ŁA�Ȑ��F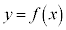 ����㑤�̕����ɂȂ�܂��B
����㑤�̕����ɂȂ�܂��B
�s�����F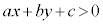 �̕\���̈�́A
�̕\���̈�́A
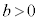 �ł���A
�ł���A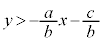 ���A�����F
���A�����F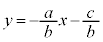 ���㑤�̕���
���㑤�̕���
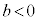 �ł���A
�ł���A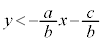 ���A�����F
���A�����F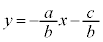 ��艺���̕���
��艺���̕���
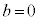 �C
�C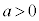 �ł���A
�ł���A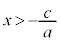 ���A�����F
���A�����F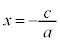 ���E���̕���
���E���̕���
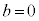 �C
�C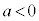 �ł���A
�ł���A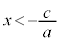 ���A�����F
���A�����F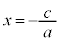 ��荶���̕���
��荶���̕���
�s�����F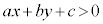 �̕\���̈���A�����F
�̕\���̈���A�����F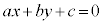 �����̈��ƌ����܂��B
�����̈��ƌ����܂��B
�s�����F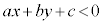 �̕\���̈���A�����F
�̕\���̈���A�����F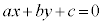 �����̈��ƌ����܂��B
�����̈��ƌ����܂��B
��ʂɁA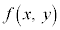 ��x�Cy���܂ގ��Ƃ��āA�Ȑ��F
��x�Cy���܂ގ��Ƃ��āA�Ȑ��F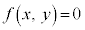 ���l����Ƃ��A
���l����Ƃ��A
�s�����F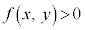 �̕\���̈���A�Ȑ��F
�̕\���̈���A�Ȑ��F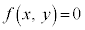 �̐��̈�ƌ����܂��B
�̐��̈�ƌ����܂��B
�s�����F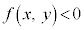 �̕\���̈���A�Ȑ��F
�̕\���̈���A�Ȑ��F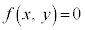 �̕��̈�ƌ����܂��B
�̕��̈�ƌ����܂��B
�s�����F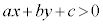 �̕\���̈�����W���ʏ�ɐ}��������ŁAa�Cb�̐����ɂ��A�̈悪�����̏ゾ������A����������A�E��������A���������肷��̂ŁA�~�X��}���邽�߂ɁA�ȉ��̂悤�ɂ��ė̈�}�����s���܂��B
�̕\���̈�����W���ʏ�ɐ}��������ŁAa�Cb�̐����ɂ��A�̈悪�����̏ゾ������A����������A�E��������A���������肷��̂ŁA�~�X��}���邽�߂ɁA�ȉ��̂悤�ɂ��ė̈�}�����s���܂��B
������ɂȂ��_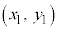 ��1�I�т܂�(�Ȃ�ׂ��ȒP�ȍ��W��I�Ԃ���)�B
��1�I�т܂�(�Ȃ�ׂ��ȒP�ȍ��W��I�Ԃ���)�B
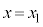 �C
�C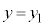 ��s�����ɑ�����āA
��s�����ɑ�����āA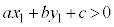 �����藧�ĂA
�����藧�ĂA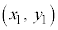 �͗̈���̓_�ł��B�̈��}������ꍇ�ɂ́A�����F
�͗̈���̓_�ł��B�̈��}������ꍇ�ɂ́A�����F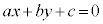 �Ɋւ��āA�_
�Ɋւ��āA�_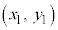 ���܂ޑ��Ɏΐ������܂��B
���܂ޑ��Ɏΐ������܂��B
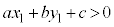 �����藧���Ȃ���A
�����藧���Ȃ���A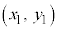 �͗̈�O�̓_�ł��B�����F
�͗̈�O�̓_�ł��B�����F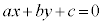 �Ɋւ��āA�_
�Ɋւ��āA�_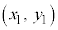 ���܂܂Ȃ����Ɏΐ������܂��B
���܂܂Ȃ����Ɏΐ������܂��B
 ��D
��D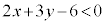 �̕\���̈��}�����܂��B
�̕\���̈��}�����܂��B
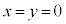 ��������ƁA
��������ƁA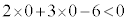 �ƂȂ�A�s��������������̂ŁA
�ƂȂ�A�s��������������̂ŁA
�����F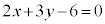 �Ɋւ���
�Ɋւ���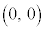 �Ɠ����������߂�̈�ƂȂ�܂��B
�Ɠ����������߂�̈�ƂȂ�܂��B
�}������ƁA�E�}�F�ΐ���(���E�����܂܂Ȃ�)�B
��ʂɁA�s�����F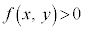 �̕\���̈��}������̂ɁA�Ȑ��F
�̕\���̈��}������̂ɁA�Ȑ��F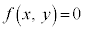 ��ɂȂ��_
��ɂȂ��_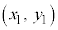 ������Ă��āA
������Ă��āA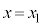 �C
�C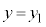 ��s�����ɑ�������Ƃ��ɁA
��s�����ɑ�������Ƃ��ɁA
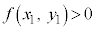 ����������Ȃ�A�_
����������Ȃ�A�_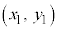 �͗̈���̓_�ł��B�Ȑ��F
�͗̈���̓_�ł��B�Ȑ��F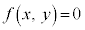 �Ɋւ��āA�_
�Ɋւ��āA�_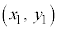 ���܂ޑ��Ɏΐ������܂��B
���܂ޑ��Ɏΐ������܂��B
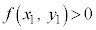 ���������Ȃ��Ȃ�A�_
���������Ȃ��Ȃ�A�_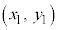 �͗̈�O�̓_�ł��B�Ȑ��F
�͗̈�O�̓_�ł��B�Ȑ��F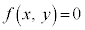 �Ɋւ��āA�_
�Ɋւ��āA�_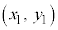 ���܂܂Ȃ����Ɏΐ������܂��B
���܂܂Ȃ����Ɏΐ������܂��B
���W���ʏ�ŁA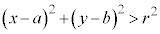 �̕\���̈�́A�~�F
�̕\���̈�́A�~�F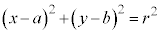 ���O���ł��B
���O���ł��B
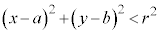 �̕\���̈�́A�~�F
�̕\���̈�́A�~�F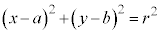 �������ł��B
�������ł��B
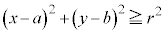 �̕\���̈�́A�~�F
�̕\���̈�́A�~�F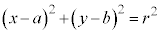 ����O���ł�(�~������܂�)�B
����O���ł�(�~������܂�)�B
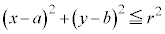 �̕\���̈�́A�~�F
�̕\���̈�́A�~�F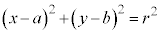 ��������ł�(�~������܂�)�B
��������ł�(�~������܂�)�B
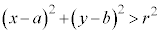 �̕\���̈�́A�~�̒��S
�̕\���̈�́A�~�̒��S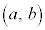 �̍��W�A
�̍��W�A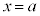 �C
�C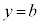 ��s�����ɑ������Ɛ��藧���Ȃ��̂ŁA���S���܂܂Ȃ����ƂȂ�A�~�F
��s�����ɑ������Ɛ��藧���Ȃ��̂ŁA���S���܂܂Ȃ����ƂȂ�A�~�F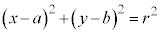 ���O���ł��B
���O���ł��B
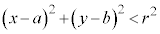 �̕\���̈�́A
�̕\���̈�́A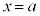 �C
�C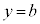 ��s�����ɑ������Ɛ��藧�̂ŁA���S���܂ޑ��ƂȂ�A�~�F
��s�����ɑ������Ɛ��藧�̂ŁA���S���܂ޑ��ƂȂ�A�~�F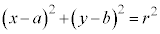 �������ł��B
�������ł��B
�����̑�����(���́Ax�Cy�̊W���ł���A�������łȂ��Ă��悢)�F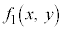 �C
�C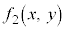 �C����C
�C����C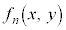 �̐ςɈ������������悤�Ȏ��̐����ŕ\�����s�����A�Ⴆ�A
�̐ςɈ������������悤�Ȏ��̐����ŕ\�����s�����A�Ⴆ�A
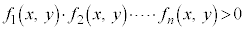 ����@
����@
�ŕ\�����̈��}������Ƃ�(�e�������F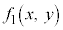 �C
�C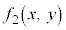 �C����C
�C����C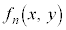 �́A����������̒l�����̒l����蓾�鑽�������Ƃ��܂�)�ɂ́A�ȉ��̂悤�ɍs���܂��B
�́A����������̒l�����̒l����蓾�鑽�������Ƃ��܂�)�ɂ́A�ȉ��̂悤�ɍs���܂��B
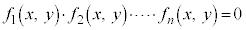 �����E����^���܂��B
�����E����^���܂��B
�܂��A���E���F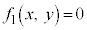 �C
�C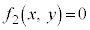 �C����C
�C����C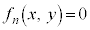 ���������݂܂��B
���������݂܂��B
�e���E����ɗ��Ȃ��_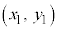 ��1�I�т܂��B
��1�I�т܂��B
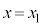 �C
�C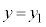 ��s�����@�ɑ�����܂��B
��s�����@�ɑ�����܂��B
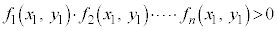 �����藧�ĂA
�����藧�ĂA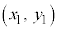 �͗̈���̓_�ł��B�_
�͗̈���̓_�ł��B�_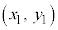 ���܂ޗ̈�Ɏΐ������܂��B
���܂ޗ̈�Ɏΐ������܂��B
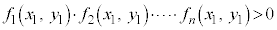 �����藧���Ȃ��Ƃ��́A
�����藧���Ȃ��Ƃ��́A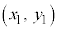 �͗̈�O�̓_�ł��B�_
�͗̈�O�̓_�ł��B�_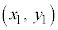 ���܂ޗ̈�ɂ͎ΐ��͓���܂���B
���܂ޗ̈�ɂ͎ΐ��͓���܂���B
���̌�́A����̈�Ɏΐ�������ꍇ�ɂ́A���E������ėאڂ���̈�ɂ͎ΐ�����ꂸ�A
����̈�Ɏΐ�������Ȃ��ꍇ�ɂ́A���E������ėאڂ���̈�Ɏΐ������܂��B
���ǁA�s���͗l�̂悤�ɁA�݂��Ⴂ�Ɏΐ������銴���ɂȂ�܂��B
�s�����F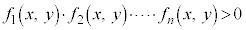 �̕\���̈�ł͋��E�����܂݂܂���B
�̕\���̈�ł͋��E�����܂݂܂���B
�s�����F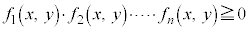 �̕\���̈�ł͋��E�����܂݂܂��B
�̕\���̈�ł͋��E�����܂݂܂��B
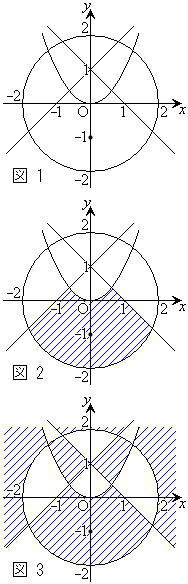 ��D�s�����F
��D�s�����F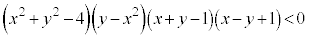 �̕\���̈��}�����܂��B
�̕\���̈��}�����܂��B
���E���́A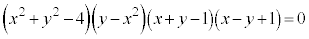 �Ƃ��āA
�Ƃ��āA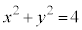 �C
�C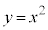 �C
�C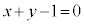 �C
�C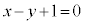
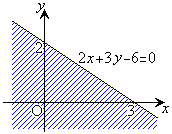
������A���W���ʏ�ɏ������݂܂�(�E�}�A�}1)�B
���E����ɗ��Ȃ��_��1�A�Ⴆ��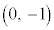 ��I�т܂��B
��I�т܂��B
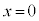 �C
�C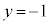 ��s�����ɑ�����܂��B
��s�����ɑ�����܂��B
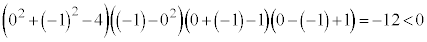
�ƂȂ�̂ŁA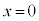 �C
�C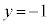 �́A�^�s���������܂��B
�́A�^�s���������܂��B
�Ƃ������Ƃ́A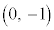 �͗̈���̓_�ł��B
�͗̈���̓_�ł��B
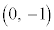 ���܂ޗ̈�Ɏΐ������܂�(�E�}�A�}2)�B
���܂ޗ̈�Ɏΐ������܂�(�E�}�A�}2)�B
�~�F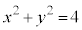 �C�������F
�C�������F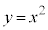 �C�����F
�C�����F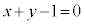 �C�����F
�C�����F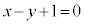 ����ėאڂ���̈�ɂ͎ΐ��͓���܂���B
����ėאڂ���̈�ɂ͎ΐ��͓���܂���B
�Ȍ�́A���E�����܂������ƂɁA�ΐ��̓���A����Ȃ����݂��Ⴂ�ɂȂ�悤�Ɏΐ������Ă䂫�܂��B
���߂�̈�́A�E�}�̐}3 �F�ΐ���(���E���͊܂܂Ȃ�)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B