2直線の交点 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
連立方程式：
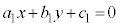･･･①
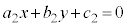･･･②
を連立して解くことを考えます。
①×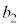
－②×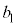
によりyを消去すると、
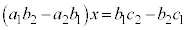
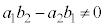であれば、
(
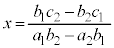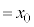とおく)
①に代入すると、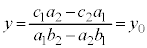
(
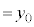とおく)
連立方程式の解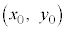
は、①に代入しても②に代入しても成り立ちます。
これは、点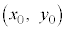
が直線①上の点であるとともに、直線②上の点であることを意味しています。
直線①上の点であって、直線②上の点でもある点とは、直線①と直線②の交点に他なりません。
連立方程式の解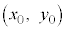
を求めるときに、
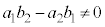という条件がつきましたが、
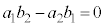⇔ 直線①と直線②が平行
なので、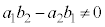
は、2直線①と②が平行でないということを意味しています。
①と②を連立して解くということは、2直線①と②が平行でなければ、直線①と直線②の交点を求めることにほかなりません。
①と②が平行な場合には、2直線はそもそも共有点を持たないか(連立方程式の解はなく、「不能」)、あるいは、①と②が同一の直線の方程式となり、直線上の全ての点の座標が解になる(連立方程式の解は無数に存在して「不定」)かのどちらかになります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。