���嗝�n���w'09�N��[2]
���ʏ�̉s�p�O�p�`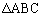 �̓���(�ӂⒸ�_�͊܂܂Ȃ�)�ɓ_P���Ƃ�A
�̓���(�ӂⒸ�_�͊܂܂Ȃ�)�ɓ_P���Ƃ�A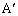 ��B�CC�CP��ʂ�~�̒��S�A
��B�CC�CP��ʂ�~�̒��S�A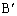 ��C�CA�CP��ʂ�~�̒��S�A
��C�CA�CP��ʂ�~�̒��S�A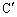 ��A�CB�CP��ʂ�~�̒��S�Ƃ���B���̂Ƃ�A�CB�CC�C
��A�CB�CP��ʂ�~�̒��S�Ƃ���B���̂Ƃ�A�CB�CC�C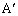 �C
�C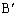 �C
�C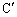 ������~����ɂ��邽�߂̕K�v�\��������P��
������~����ɂ��邽�߂̕K�v�\��������P��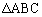 �̓��S�Ɉ�v���邱�Ƃł��邱�Ƃ������B
�̓��S�Ɉ�v���邱�Ƃł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�\�����F�uP��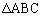 �̓��S�v�ˁuA�CB�CC�C
�̓��S�v�ˁuA�CB�CC�C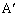 �C
�C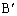 �C
�C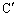 ������~����v
������~����v
�̕��͂����ł����A
�K�v���F�uA�CB�CC�C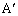 �C
�C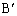 �C
�C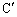 ������~����v�ˁuP��
������~����v�ˁuP��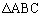 �̓��S�v
�̓��S�v
���Ȃ��Ȃ����ł��B
�K�v���������Ƃ��ɁAP�����S�ł��邱�Ƃ�AA�CP�C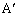 ���꒼����ɂ��邱�Ƃ�O��Ƃ��Ȃ��悤�ɒ��ӂ��܂��傤�B
���꒼����ɂ��邱�Ƃ�O��Ƃ��Ȃ��悤�ɒ��ӂ��܂��傤�B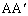 ��
��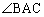 �̓����ł��邱�Ƃ͊ȒP�Ɍ����܂����AP��
�̓����ł��邱�Ƃ͊ȒP�Ɍ����܂����AP��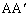 ��ɂ͑��݂��Ȃ��Ƃ�������(���ł���)�ɗ����Ę_����悤�ɂ��܂��B
��ɂ͑��݂��Ȃ��Ƃ�������(���ł���)�ɗ����Ę_����悤�ɂ��܂��B
�܂��A�_P�̂܂��Ŋp���l����ƁA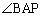 �C
�C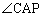 �ȂǂƂ��܂����т����ɍl���ɂ����Ȃ�܂��B
�ȂǂƂ��܂����т����ɍl���ɂ����Ȃ�܂��B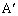 ��B�CC�CP��ʂ�~�̒��S�Ƃ���A�Ƃ������Ƃ́A
��B�CC�CP��ʂ�~�̒��S�Ƃ���A�Ƃ������Ƃ́A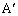 �͎O�p�`BCP�̊O�S���ƌ������Ƃł��B�O�S�͊e�ӂ̐��������̌�_�Ȃ̂ŁA���̐��������Ƃ̊Ԃɂł���p���l����悤�ɂ��܂��B
�͎O�p�`BCP�̊O�S���ƌ������Ƃł��B�O�S�͊e�ӂ̐��������̌�_�Ȃ̂ŁA���̐��������Ƃ̊Ԃɂł���p���l����悤�ɂ��܂��B
A�CB�CC�C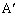 �C
�C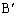 �C
�C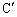 ������~����ɂ���Ƃ��܂�(���̉~��D�Ƃ��܂�)�B
������~����ɂ���Ƃ��܂�(���̉~��D�Ƃ��܂�)�B
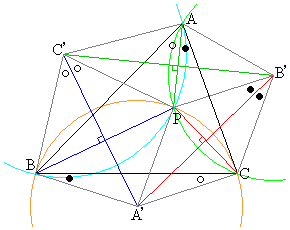 �O�p�`ABC�̓����̓_P�ɑ��āA
�O�p�`ABC�̓����̓_P�ɑ��āA
B�CC�CP��ʂ�~�̒��S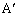 �́APB�̐���������PC�̐��������̌�_�ł��B
�́APB�̐���������PC�̐��������̌�_�ł��B
C�CA�CP��ʂ�~�̒��S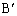 �́APC�̐���������PA�̐��������̌�_�ł��B
�́APC�̐���������PA�̐��������̌�_�ł��B
A�CB�CP��ʂ�~�̒��S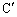 �́APA�̐���������PB�̐��������̌�_�ł��B
�́APA�̐���������PB�̐��������̌�_�ł��B
�~D�ɂ��āA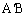 ��ɗ��~���p�͓������̂ŁA
��ɗ��~���p�͓������̂ŁA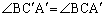
�܂��A�O�p�`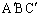 �ƎO�p�`
�ƎO�p�`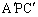 �͍����Ȃ̂ŁA
�͍����Ȃ̂ŁA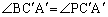
�܂�A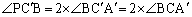
�܂��AA�AB�CP��ʂ�~�ɂ��āAPB�̏�ɗ����S�p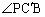 �͉~���p
�͉~���p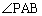 ��2�{�ł��B
��2�{�ł��B
�܂�A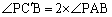
�� 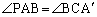 �@����@
�@����@
�~D�ɂ��āA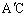 ��ɗ��~���p�͓������̂ŁA
��ɗ��~���p�͓������̂ŁA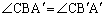
�܂��A�O�p�`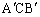 �ƎO�p�`
�ƎO�p�`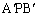 �͍����Ȃ̂ŁA
�͍����Ȃ̂ŁA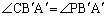
�܂�A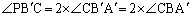
�܂��AC�CA�CP��ʂ�~�ɂ��āAPC�̏�ɗ����S�p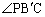 �͉~���p
�͉~���p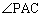 ��2�{�ł��B
��2�{�ł��B
�܂�A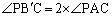
�� 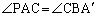 �@����A
�@����A
�܂��A�O�p�`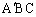 �́A
�́A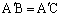 �ł���ӎO�p�`�Ȃ̂ŁA
�ł���ӎO�p�`�Ȃ̂ŁA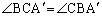
����ƁA�@�C�A���A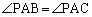
���l�ɂ��āA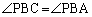 �C
�C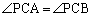
����āA�_P�͎O�p�`ABC�̓��S�ł��B
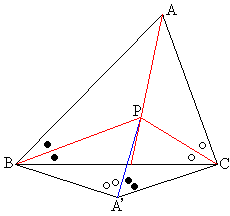 P��
P��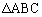 �̓��S���Ƃ��܂��B
�̓��S���Ƃ��܂��B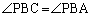 �C
�C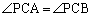
�ł��B
�܂��A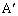 �𒆐S�Ƃ��AB�CC�CP��ʂ�~�ɂ��āAPB�̏�ɗ����S�p
�𒆐S�Ƃ��AB�CC�CP��ʂ�~�ɂ��āAPB�̏�ɗ����S�p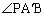 �͉~���p
�͉~���p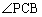 ��2�{�ł��B
��2�{�ł��B
���l�ɁAPC�̏�ɗ����S�p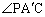 �͉~���p
�͉~���p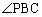 ��2�{�ł��B
��2�{�ł��B
�O�p�`�̓��p�̘a��π�Ȃ̂ŁA
����āA�Ό����钸�p���݂��ɕ�p���Ȃ��̂ŁA�l�p�`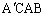 �͉~�ɓ��ڂ���l�p�`�ł��B
�͉~�ɓ��ڂ���l�p�`�ł��B
���l�ɂ��āA�l�p�`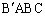 �C�l�p�`
�C�l�p�`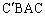 ���~�ɓ��ڂ���l�p�`�ł��B
���~�ɓ��ڂ���l�p�`�ł��B
3�̎l�p�`�̊O�ډ~�́A��������O�p�`ABC�̊O�ډ~�ł����ē���̉~�ł��B
�]���āAA�CB�CC�C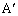 �C
�C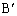 �C
�C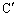 �͓���~����ɂ���܂��B
�͓���~����ɂ���܂��B
�ȏ���AA�CB�CC�C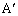 �C
�C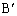 �C
�C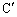 ������~����ɂ��邽�߂��K�v�\�������́A�uP��
������~����ɂ��邽�߂��K�v�\�������́A�uP��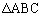 �̓��S�Ɉ�v���邱�Ɓv�ł��B
�̓��S�Ɉ�v���邱�Ɓv�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B