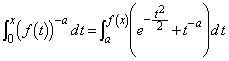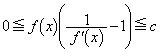���s��w���w�ߋ���W [1] �@ α �C β �C γ �� ('99 ��� [2]) [2] �@ a �C m �͎��R���� a �͒萔�Ƃ���B xy ���ʏ�̓_ x ���ň͂܂��̈�̖ʐς� xy ���ʏ�̊i�q�_�Ƃ͂��̓_�� x ���W�� y ���W���Ƃ��ɐ����ƂȂ�_�̂��Ƃł���B ('98 �O�� [4]) [3] �@ n �� 3 �ȏ�̐����Ƃ���B�~����� n �����_�̂���_���o���_�Ƃ��A n �����_�����̕����Ɏ��̂悤�ɐi�ށB �e�_�ŃR�C���𓊂��A�\���o��Ύ��̓_�ɐi�݁A�����o��Ύ��̓_�щz�����̎��̓_�ɐi�ށB
(1) �ŏ��� 1 ���܂�����Ƃ��A�o���_�щz���m�� (2) k �� 2 �ȏ�̐����Ƃ���B k ���ڂɏ��߂ďo���_�ފm���� ('96 �O�� [6]) [4] �@ a �C b �� p �C d �͑f���� d �� 1 �ł��邱�Ƃ������B ('95 �N�O�� [2]) [5] �@ a �C b �C c �͎����� �C �Ƃ����B x �ɑ��� x �ɑ��� ('95 �N��� [3]) [6] �@ n �� 0 �܂��͐��̐����Ƃ���B �ɂ���Ē�߂�B 3 �Ŋ������]��� �Ƃ����B (1) �C�������C (2) �ł��邱�Ƃ������B (3) �����藧���Ƃ������B ('94 �O�� [2]) [7] �@ �� 4 �ʑ̂� 4 �̒��_�� A �C B �C C �C D �Ƃ���B s �C t �� ���� AB �� s �F E �C AC �� t �F F �C AD �� t �F G �Ƃ����B 3 �_ E �C F �C G ��ʂ镽�ʂ��A 3 �_ B �C C �C D ��ʂ�~�Ƌ��L�_�������߂� s �C t �̖������ׂ����������߁A�_ ('94 �N�O�� [3]) [8] �@ a �͐��̒萔�Ƃ���B�s���� �����ׂĂ̐��̐� x �ɑ��Đ��藧�Ƃ����B���̂Ƃ��A a �͂ǂ̂悤�Ȃ��̂��B ('93 ��� [4]) [9] �@ θ �� (1) ���� θ �����߂�B (2) m �C n �� 0 �ȏ�̐����Ƃ���B θ �ɂ��Ă̕�����
���������Ƃ��� θ �����߂�B ('92 �N�O�� [2]) [10] �@���� a �C b (�C ) �ɑ��A���̕s���������藧���Ƃ������B ('91 �O�� [4]) [11] �@�� ( �͎��̏����@�C�A�����Ă���B �@ �͔����\�� ���̒萔 a �������āA (1) �A�̓����̗��ӂ� x �ɂ��Ĕ������ē����� (y �C ) �W���������B�܂��A (2) ���̒萔 b �C c �������Ď��̕s���� ( �C ) �C ( �� ) �����Ă��邱�Ƃ������B
( �C ) �@ ( �� ) (3) �����߂�B�܂��A ('91 �O�� [6]) [12] �@�l�ʑ� OABC �ɂ����āA G ��ʂ� OPABC �̐���́A�ǂ̂悤�Ȑ}�`���B a �C b �C c �̊W�ɂ��敪���ďq�ׂ�B ('89 �N�O�� [4]) [13] �@���� 10m �̉~���`�̓��������^���N������A�~���̒�ʂ������ɂ����Đ����ł���悤�ɒu����Ă���B�^���N���̐��� ( ���̐[�� ) �� y m (�̂Ƃ��ɂ� l /���̑��x�Œ������邱�Ƃɂ���B�^���N����̂Ƃ��ɒ������n�߂āA 9 ���Ԍ�ɐ��ʂ� 2m �ɂȂ����B�^���N�ɐ�����t�ɂȂ�̂́A���Ɖ����Ԍォ�B ('89 �N�O�� [6]) [14] �@�`�C B �C C �� 3 �l�����āA���ꂼ��A�ԎD�Ɣ��D�� 1 ���������Ă���B���̏�Ԃ���o�����āA���̂悤�ȎD�̈ړ������s���B A �� B �ɁA B �� C �ɁA C �� A �ɁA�����Ă��� 2 ���̎D�̂��� 1 ����ׂɑI��ŁA�����ɓn���B (1) ���̈ړ��̌�A�N���肤��D�̏�Ԃ�S�������グ�A������ �Ƃ����悤�ɋL��������B�������A�ŏ��̏�Ԃɂ� (2) ��œ����e��� 1 ��̈ړ��� (3) �ŏ��̏�Ԃ��� n ��ړ������Ƃ��A ('87 �N [6]) [15] �@���ꕽ�ʏ�� 2 �̎O�p�`�� ABC �C�� 1 �ł���Ƃ���B���� 2 �̊O�ډ~�̒��S�����Ԑ����̒��_�� M �C���� P �C Q �C R �Ƃ���B (2) ������ PQR ���s�p�O�p�`�ł��̊O�ډ~�̔��a�� 1 �ƂȂ�Ȃ�A�_ M �͂��̊O�ډ~�̒��S�ƈ�v���邱�Ƃ������B����ɁA���̂Ƃ��� ABC �C�� PQR �͂��ׂč����ƂȂ邱�Ƃ������B ('86 �N [4]) [16] �@ b �C c �͎����Ƃ��A 2 ���� α �C β �Ƃ���B (1) �C γ �ɑ��Ă� t �C u �����݂��邱�Ƃ������B (2) �Ƃ����Ƃ��A���̏��� ( �� ) �����_ �c �����肵�A�}������B ( �� ) t �C u ���Ƃ��Ɏ����Ȃ�A ('85 �N [3]) [17] �@�萔 c (�ɑ��āA���� x �ɂ��Đ��藧�Ƃ��A�� c �̂����̍ŏ��l�� (1) (2) (3) ('84 �N [2]) �@�@ ���嗝�n���w TOP �@�@ ���w TOP �@�@ TOP �y�[�W�ɖ߂� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠�� © 2005-2024 (�L)����� ��w�y�w�m ���������t���I ���n��w�l�b�g�m ��w�y�w�m (���ē��������� )������́A������܂Ń��[�� ��