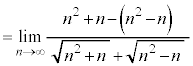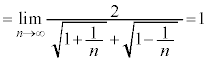数列の極限 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
無限に項が続く数列を無限数列と言います。
一般項が、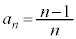 で与えられる無限数列では、
で与えられる無限数列では、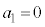 ,
,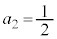 ,
,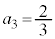 ,
,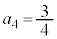 ,・・・,
,・・・,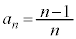 ,・・・ として、nをどんどん大きくしていくと、どんどん1に近づいていきます。
,・・・ として、nをどんどん大きくしていくと、どんどん1に近づいていきます。
このように、数列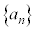 において、nを限りなく大きくしていくときに、
において、nを限りなく大きくしていくときに、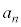 の値が限りなくある値αに近づくとき、
の値が限りなくある値αに近づくとき、
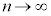 のとき、
のとき、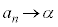
または、
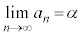
と書いて、数列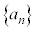 はαに収束すると言います。また、値αを極限値と言います。
はαに収束すると言います。また、値αを極限値と言います。
数列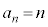 においては、
においては、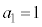 ,
,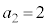 ,
,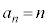 ,
,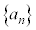 ,・・・,
,・・・,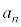 ,・・・ として、nをどんどん大きくしていくと、どんどん0に近づいていきます。よって、
,・・・ として、nをどんどん大きくしていくと、どんどん0に近づいていきます。よって、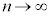 ,
,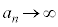 です。
です。
一般項が、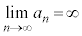 で与えられる無限数列では、
で与えられる無限数列では、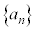 ,
,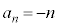 ,・・・,
,・・・,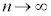 ,・・・ として、nをどんどん大きくしていくと、どんどん大きな値になっていきます。
,・・・ として、nをどんどん大きくしていくと、どんどん大きな値になっていきます。
このように、数列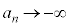 において、nを限りなく大きくしていくときに、
において、nを限りなく大きくしていくときに、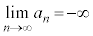 の値が限りなく大きくなるとき、
の値が限りなく大きくなるとき、
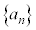 のとき、
のとき、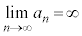
または、
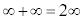
と書いて、数列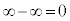 は正の無限大に発散すると言います。このときには極限値はありません。
は正の無限大に発散すると言います。このときには極限値はありません。
一般項が、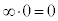 で与えられるような数列の場合には、nをどんどん大きくしていくと、負の数で絶対値がどんどん大きくなっていきます。
で与えられるような数列の場合には、nをどんどん大きくしていくと、負の数で絶対値がどんどん大きくなっていきます。
このような場合には、
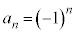 のとき、
のとき、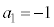
または、
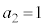
と書いて、数列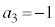 は負の無限大に発散すると言います。このときには極限値はありません。
は負の無限大に発散すると言います。このときには極限値はありません。
注.無限大記号‘∞'は、「限りなく大きくなる」ことを表す記号であって、値ではありません。従って、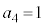 となる場合の‘∞'を極限値とは言いません。また、
となる場合の‘∞'を極限値とは言いません。また、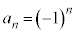 ,
,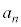 ,
,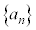 などとするのは誤りです。
などとするのは誤りです。
一般項が、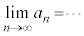 で与えられる無限数列では、
で与えられる無限数列では、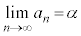 ,
,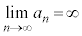 ,
,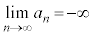 ,
,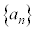 ,・・・,
,・・・,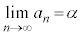 ,・・・ として、nをどんどん大きくしていっても、
,・・・ として、nをどんどん大きくしていっても、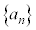 がある値に近づくわけではありません。
がある値に近づくわけではありません。
このような場合には、数列 は振動すると言います。振動する場合も含めて、発散と言います。
は振動すると言います。振動する場合も含めて、発散と言います。
振動する場合には、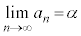 のように書きようがありません。この場合には、極限はない、と言います。極限値もありません。
のように書きようがありません。この場合には、極限はない、と言います。極限値もありません。
それに対して、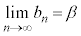 の場合には、極限値がαであるとともに、極限はαという言い方もします。
の場合には、極限値がαであるとともに、極限はαという言い方もします。
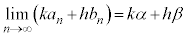 の場合には、極限は正の無限大、
の場合には、極限は正の無限大、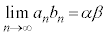 の場合には、極限は負の無限大、と言います。
の場合には、極限は負の無限大、と言います。
以上を整理すると下記のようになります。
数列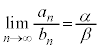 が収束する場合、
が収束する場合、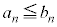 ,極限,極限値はα
,極限,極限値はα
数列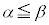 が発散する場合、
が発散する場合、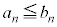
極限の性質
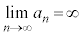 ,
,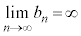 のとき、k,hを実数として、
のとき、k,hを実数として、
(線形性) 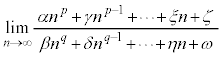
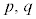 ,
,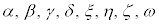
すべての自然数nについて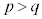 であれば、
であれば、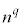
すべての自然数nについて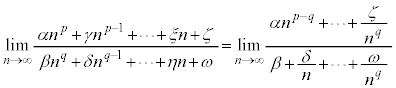 であって、
であって、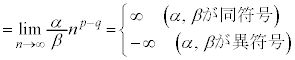 であれば、
であれば、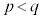
例1.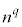 (
(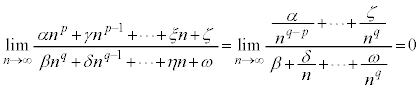 は自然数,
は自然数,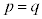 は実数)
は実数)
・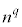 の場合、分母分子を
の場合、分母分子を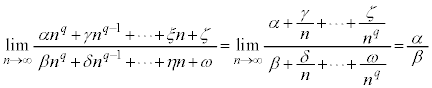 で割ると、
で割ると、
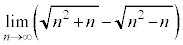
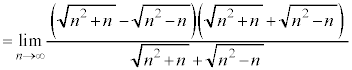 (分子の方が強い)
(分子の方が強い)
・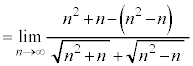 の場合、分母分子を
の場合、分母分子を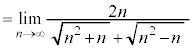 で割ると、
で割ると、
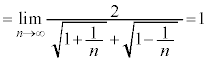 (分母の方が強い)
(分母の方が強い)
・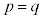 の場合、分母分子を
の場合、分母分子を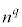 で割ると、
で割ると、
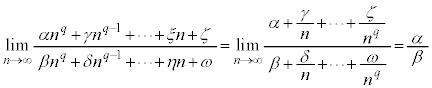 (分母分子の最高次の項の係数が残ります)
(分母分子の最高次の項の係数が残ります)
例2.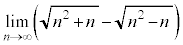
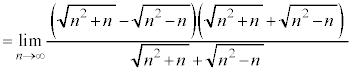 (和差公式を利用する)
(和差公式を利用する)
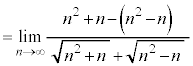
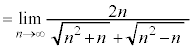 (分母分子をnで割る)
(分母分子をnで割る)
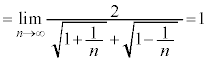
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 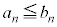
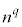 (
(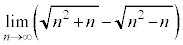
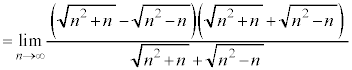 (分子の方が強い)
(分子の方が強い)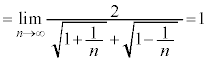 (分母の方が強い)
(分母の方が強い)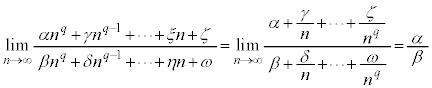 (分母分子の最高次の項の係数が残ります)
(分母分子の最高次の項の係数が残ります)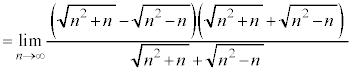 (和差公式を利用する)
(和差公式を利用する)