平面と直線 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
令和3年の数学Aの教科書には、取って付けたように「空間図形」という項目が入っていますが、数学Bの空間ベクトルと同じ扱いで良いと思います。数学Ⅰ・Aのみが試験範囲の受験生は教科書をよく読んでおいてください。
ここでは、ベクトルを使って考えます。
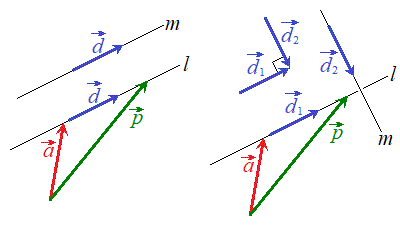
・直線
直線の方向ベクトルを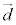 ,起点ベクトル(直線上の1点を指定するベクトル)を
,起点ベクトル(直線上の1点を指定するベクトル)を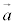 ,また、t を実数として、直線上の点の位置ベクトル
,また、t を実数として、直線上の点の位置ベクトル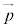 は、
は、 と表されます。
・2直線の平行
方向ベクトルが等しい2直線l,mが異なる直線のとき、lとmは平行(l // m)です。 ・・・(*)
・2直線の垂直
2直線をl: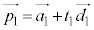 ,m:
,m: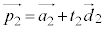 とし、その方向ベクトル
とし、その方向ベクトル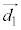 ,
,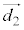 について、
について、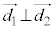 ,つまり、
,つまり、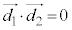 のとき、lとmは垂直(
のとき、lとmは垂直(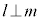 )です。
)です。
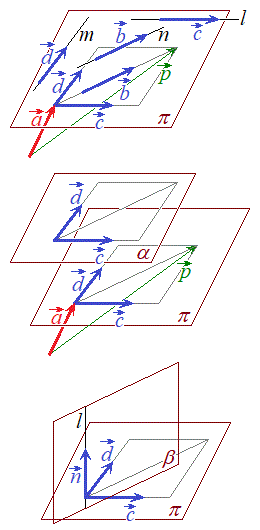 ・平面
・平面平面は、方向ベクトルを2つ持つように考えます。2つの1次独立なベクトルを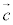 ,
,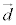 ,起点ベクトル(平面上の1点を指定するベクトル)を
,起点ベクトル(平面上の1点を指定するベクトル)を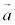 ,また、s,tを実数として、平面上の点の位置ベクトル
,また、s,tを実数として、平面上の点の位置ベクトル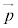 は、
は、 と表されます。この平面をπ(円周率ではありません)とします。
・平面と平行な直線
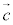 を方向ベクトルとする直線l:
を方向ベクトルとする直線l: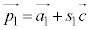 (
(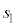 :実数),
:実数),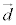 を方向ベクトルとする直線m:
を方向ベクトルとする直線m: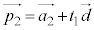 (
(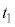 :実数)は、πと平行(l // π,m // π)です。一般的に、
:実数)は、πと平行(l // π,m // π)です。一般的に、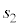 ,
,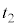 を実数の定数として、
を実数の定数として、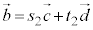 を方向ベクトルとする直線n:
を方向ベクトルとする直線n: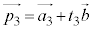 (
(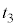 :実数)は、πと平行(n // π)です。但し、l,m,nは平面π上の直線ではない、とします。
:実数)は、πと平行(n // π)です。但し、l,m,nは平面π上の直線ではない、とします。・2平面の平行
q,rを実数として、平面πと共通のベクトル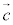 ,
,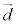 を用いて、
を用いて、 α: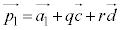
のように表される平面αが平面πと異なる平面であるとき、αとπは平行(α // π)です。
・平面と垂直な直線
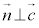 ,
,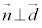 となるベクトル
となるベクトル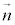 (例えば、
(例えば、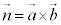 ,×は外積)を方向ベクトルとする直線l:
,×は外積)を方向ベクトルとする直線l: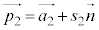 (
(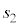 :実数)は、πと垂直(
:実数)は、πと垂直(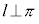 )です。
)です。・2平面の垂直
と表される平面βはπと垂直(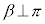 )です。
)です。
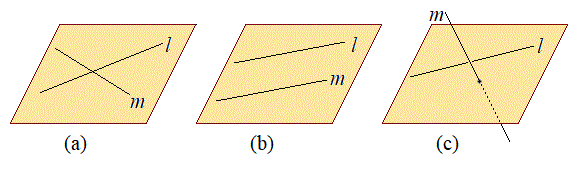 (1) 2直線の位置関係
(1) 2直線の位置関係l: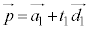 (
(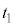 :実数) ・・・①m:
:実数) ・・・①m: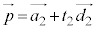 (
(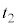 :実数) ・・・②
:実数) ・・・② (a) 2直線が交わる
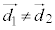 であり、①,②を連立すると、解
であり、①,②を連立すると、解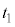 ,
,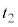 を持ちます。そのときの
を持ちます。そのときの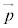 が交点の位置ベクトルです。
が交点の位置ベクトルです。(b) 2直線が平行(l // m)
上記(*)により、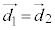 です。①,②を連立しても、
です。①,②を連立しても、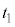 ,
,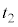 の解は存在しません。
の解は存在しません。 (c) ねじれの位置にある
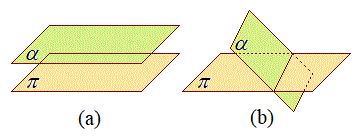 (2) 2平面の位置関係
(2) 2平面の位置関係(a) 2平面が平行(α // π)
2平面に共有点はありません。
(b) 2平面が交わる
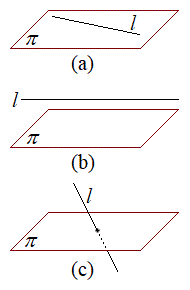 (3) 直線と平面の位置関係
(3) 直線と平面の位置関係(a) 平面が直線を含む
直線の方向ベクトルを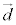 ,t を実数として、
,t を実数として、 l: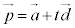
とすると、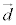 と1次独立なベクトルを
と1次独立なベクトルを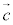 として、直線lを含む平面は、
として、直線lを含む平面は、 π: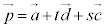 ・・・③
・・・③ と表されます。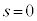 のときlと一致します。
のときlと一致します。 (b) 直線と平面が平行
直線が、方向ベクトルを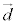 ,tを実数として、
,tを実数として、 l: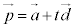 ・・・④
・・・④ とすると、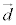 と1次独立なベクトルを
と1次独立なベクトルを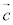 ,また、
,また、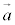 とは異なるベクトルを
とは異なるベクトルを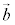 ,sを実数として、直線lと平行な平面は、
,sを実数として、直線lと平行な平面は、 π: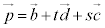 ・・・⑤
・・・⑤ と表され、④と⑤を連立したとき、s,t の解はありません。
(c) 直線が平面と1点で交わる。
l: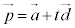 ・・・⑥π:
・・・⑥π: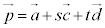 ・・・⑦
・・・⑦ ⑥,⑦を連立すると、s,t はただ1組の解をもち、そのときの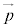 が交点の位置ベクトルになります。
が交点の位置ベクトルになります。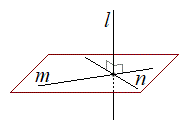 l がπ上の任意の異なる2直線m,nに対して、
l がπ上の任意の異なる2直線m,nに対して、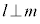 かつ
かつ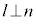 となるとき、
となるとき、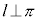 です。逆に、
です。逆に、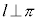 であれば、π上の任意の異なる直線mに対して
であれば、π上の任意の異なる直線mに対して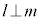 となります。
となります。
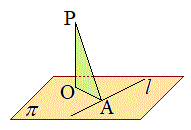 (4) 三垂線の定理:平面π上の直線lと点Oについて、Oがl上にないとき、(i)
(4) 三垂線の定理:平面π上の直線lと点Oについて、Oがl上にないとき、(i) 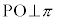 かつ
かつ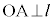 ならば、
ならば、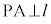 (ii)
(ii) 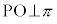 かつ
かつ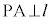 ならば、
ならば、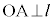 (iii)
(iii) 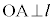 かつ
かつ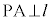 かつ
かつ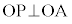 ならば、
ならば、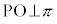
[証明] 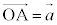 ,l:
,l: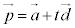 (t:実数),③より、lを含む平面π:
(t:実数),③より、lを含む平面π: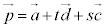 (s:実数) ・・・⑧,
(s:実数) ・・・⑧,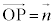 とします。
とします。 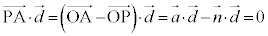 ∴
∴ 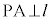
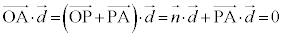 ∴
∴ 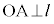
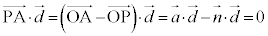 より、
より、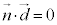
点Oは平面π上の点なので、⑧で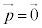 として、
として、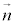 との内積をとると、
との内積をとると、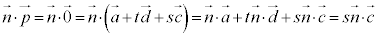 ∴
∴ 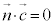
よって、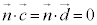 より、
より、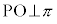
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。