�x�N�g����1���Ɨ��@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̍��ڂɂ��ẮA�x�N�g���Ƃ����Q�Ƃ��Ă��������B
(1) 2�̃x�N�g��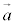 �C
�C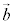 �����s�A�܂�A
�����s�A�܂�A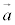 //
// 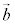 �@�́@
�@�́@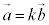 (k�F����)
(k�F����) (2) 2�̃x�N�g��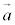 �C
�C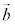 �ɂ��āA�g
�ɂ��āA�g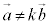 (k�F����)�@���@
(k�F����)�@���@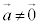 �@���@
�@���@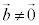 �h�ł���Ƃ��A
�h�ł���Ƃ��A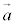 ��
��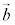 ��1���Ɨ��ł���ƌ����B
��1���Ɨ��ł���ƌ����B (3) ���ʏ��2�̃x�N�g��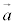 �C
�C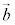 ��1���Ɨ��ł���Ƃ��A���̕��ʏ�̔C�ӂ̃x�N�g��
��1���Ɨ��ł���Ƃ��A���̕��ʏ�̔C�ӂ̃x�N�g��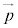 �́A
�́A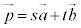 (s�Ct�͎���)�̌`�ɕ\�����Ƃ��ł���B�܂��A����s�Ct�̑g�͂���1�ʂ�ɒ�܂�B
(s�Ct�͎���)�̌`�ɕ\�����Ƃ��ł���B�܂��A����s�Ct�̑g�͂���1�ʂ�ɒ�܂�B (4) �x�N�g���́A�����������������������ł���Γ����x�N�g���ƍl���邪�A�n�_�����낦�čl������������₷���ꍇ������B�n�_�����W���ʂ̌��_O�ɂƂ��āA�x�N�g��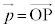 ���l����Ƃ��A
���l����Ƃ��A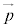 ��_P���ʒu�x�N�g���ƌ����A
��_P���ʒu�x�N�g���ƌ����A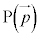 �̂悤�ɕ\���B
�̂悤�ɕ\���B
2�̃x�N�g��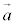 �C
�C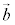 ��1���Ɨ��łȂ��Ƃ�(
��1���Ɨ��łȂ��Ƃ�(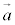 //
// 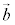 �@�܂��́@
�@�܂��́@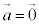 �@�܂��́@
�@�܂��́@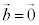 )�A
)�A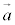 ��
��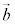 ��1���]���ł���ƌ����܂��B
��1���]���ł���ƌ����܂��B
2�̃x�N�g��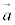 �C
�C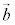 �����s�Ȃ�A�������Ⴄ���A�����������̌����Œ������Ⴄ���A�Ȃ̂ŁA����̃x�N�g���͑����̃x�N�g���̎����{�ŕ\����܂��B
�����s�Ȃ�A�������Ⴄ���A�����������̌����Œ������Ⴄ���A�Ȃ̂ŁA����̃x�N�g���͑����̃x�N�g���̎����{�ŕ\����܂��B
2�̃x�N�g��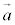 �C
�C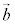 ��1���Ɨ��ł��邱�Ƃ��A�g
��1���Ɨ��ł��邱�Ƃ��A�g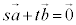 �@�́@
�@�́@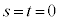 �h�ł��邱�ƁA�ƒ�`���邱�Ƃ�����܂��B
�h�ł��邱�ƁA�ƒ�`���邱�Ƃ�����܂��B
 2�̃x�N�g��
2�̃x�N�g��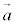 �C
�C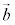 ��1���Ɨ��ł���Ƃ��A
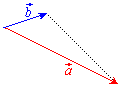
��1���Ɨ��ł���Ƃ��A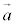 ��
��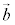 ���n�_�����낦�ď����ƉE�}�̂悤�ɎO�p�`���ł��܂��B���ʃx�N�g���ɂ����ẮA�u1���Ɨ��v�̈Ӗ����A�O�p�`����邱�Ƃ̂ł���ʒu�W�Ɗo���Ă����Ƃ悢�ł��傤�B
���n�_�����낦�ď����ƉE�}�̂悤�ɎO�p�`���ł��܂��B���ʃx�N�g���ɂ����ẮA�u1���Ɨ��v�̈Ӗ����A�O�p�`����邱�Ƃ̂ł���ʒu�W�Ɗo���Ă����Ƃ悢�ł��傤�B
(3)�������Ă����܂��B
���ʏ��2�̃x�N�g��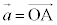 �C
�C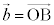 ��1���Ɨ��ł���Ƃ��A���̕��ʏ�̔C�ӂ̃x�N�g��
��1���Ɨ��ł���Ƃ��A���̕��ʏ�̔C�ӂ̃x�N�g��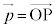 (�n�_��O�łȂ��x�N�g�����A�n�_��O�ɗ���悤�ɕ��s�ړ����čl���܂�)���Ƃ�܂��B
(�n�_��O�łȂ��x�N�g�����A�n�_��O�ɗ���悤�ɕ��s�ړ����čl���܂�)���Ƃ�܂��B
�EP������OA��̓_�Ȃ�A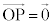 ���A�܂���
���A�܂���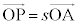 �ƕ\���܂��B
�ƕ\���܂��B 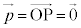 �Ȃ�A
�Ȃ�A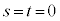 �Ƃ��āA
�Ƃ��āA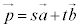 �ƕ\���܂��B
�ƕ\���܂��B
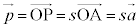 �Ȃ�A
�Ȃ�A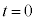 �Ƃ��āA
�Ƃ��āA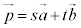 �ƕ\���܂��B
�ƕ\���܂��B�EP������OB��̓_�̏ꍇ���A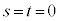 ���A�܂��́A
���A�܂��́A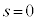 �Ƃ��āA
�Ƃ��āA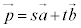 �ƕ\���܂��B
�ƕ\���܂��B 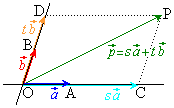 �EP������OA��ɂ��A����OB��ɂ��Ȃ��Ƃ��A�E�}�̂悤�ɁA�_P��ʂ蒼��OB�ɕ��s�Ȓ����ƒ���OA�Ƃ̌�_��C�C�_P��ʂ蒼��OA�ɕ��s�Ȓ����ƒ���OB�Ƃ̌�_��D�Ƃ���ƁA�l�p�`OCPD�͕��s�l�ӌ`�ŁA
�EP������OA��ɂ��A����OB��ɂ��Ȃ��Ƃ��A�E�}�̂悤�ɁA�_P��ʂ蒼��OB�ɕ��s�Ȓ����ƒ���OA�Ƃ̌�_��C�C�_P��ʂ蒼��OA�ɕ��s�Ȓ����ƒ���OB�Ƃ̌�_��D�Ƃ���ƁA�l�p�`OCPD�͕��s�l�ӌ`�ŁA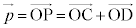 �@����@
�@����@����AC�͒���OA��̓_�Ȃ̂ŁA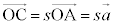 �@����A�@�ƕ\����܂��BD�͒���OB��̓_�Ȃ̂ŁA
�@����A�@�ƕ\����܂��BD�͒���OB��̓_�Ȃ̂ŁA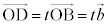 �@����B�@�ƕ\����܂��B
�@����B�@�ƕ\����܂��B
�A�C�B���@�ɑ�����邱�Ƃɂ��A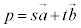 �ƕ\�����Ƃ��ł��܂��B
�ƕ\�����Ƃ��ł��܂��B �ȏ���A���ʏ��2�̃x�N�g��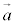 �C
�C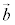 ��1���Ɨ��ł���Ƃ��A���̕��ʏ�̔C�ӂ̃x�N�g��
��1���Ɨ��ł���Ƃ��A���̕��ʏ�̔C�ӂ̃x�N�g��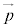 �́A
�́A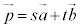 (s�Ct�͎���)�̌`�ɕ\�����Ƃ��ł��܂��B
(s�Ct�͎���)�̌`�ɕ\�����Ƃ��ł��܂��B
(3)�̌�i�ɂ��ẮA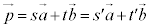 ��2�ʂ�ɕ\���ꂽ�Ƃ��܂��B
��2�ʂ�ɕ\���ꂽ�Ƃ��܂��B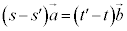 �@����C
�@����C
�����ŁA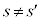 ���Ƃ���ƁA
���Ƃ���ƁA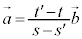 �@����D
�@����D
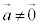 �Ȃ̂ŁA
�Ȃ̂ŁA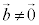 ����
����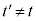 �ł����A���̂Ƃ��D�́A
�ł����A���̂Ƃ��D�́A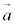 //
// 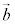 �ł��邱�Ƃ��Ӗ�����̂ŁA
�ł��邱�Ƃ��Ӗ�����̂ŁA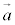 ��
��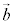 ��1���Ɨ��łȂ��Ȃ��Ă��܂��܂��B
��1���Ɨ��łȂ��Ȃ��Ă��܂��܂��B
����āA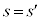 �C�C���A
�C�C���A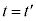
����́A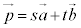 �ƂȂ����s�Ct�̑g������1�ʂ�ł��邱�Ƃ��Ӗ����܂��B
�ƂȂ����s�Ct�̑g������1�ʂ�ł��邱�Ƃ��Ӗ����܂��B
(3)�ɏo�Ă���A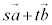 (s�Ct������)�Ƃ����`���A
(s�Ct������)�Ƃ����`���A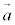 ��
��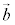 ��1�������ƌ����܂��B
��1�������ƌ����܂��B
���ʃx�N�g���̖��́A2��1���Ɨ��ȃx�N�g�����Ƃ��āA��蒆�ɓo�ꂷ��x�N�g����1�������̌`�ɕ\���čl���邱�Ƃ���{�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B