���`�v��@�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
��������1���s�����F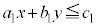 �C
�C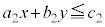 �C����C
�C����C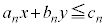
�̑S�Ă����悤��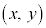 �ɑ��āA
�ɑ��āA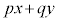 �̍ő�l�E�ŏ��l�����߂�Ƃ�����肪����B
�̍ő�l�E�ŏ��l�����߂�Ƃ�����肪����B
�e1���s�������\���̈�̋��ʕ���D��}�����Ă����A�����F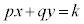 ��k�����Ē����s�ړ������A������D��ʉ߂���Ƃ���k�̍ő�l�ƍŏ��l�����߂āA
��k�����Ē����s�ړ������A������D��ʉ߂���Ƃ���k�̍ő�l�ƍŏ��l�����߂āA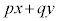 �̍ő�l�E�ŏ��l�����߂���@���A���`�v��@�ƌ����B
�̍ő�l�E�ŏ��l�����߂���@���A���`�v��@�ƌ����B
�u���`�v��@�v�́A���Ƃ��Ƃ́A�R���s���[�^�[���g���čœK���������߂邽�߂̃A���S���Y���̖��O�B
�u���`�v��@�v�ƌ������O�́A���������E���Ƃ���̈�ōl������������̂ł����A�̈�D�́A�K������1���s�����̕\���̈�łȂ��Ă��A�̈��}�����āA�����A���邢�́A�Ȑ����̈�D����ʉ߂���������l���邱�Ƃɂ��A��������͂����������܂��B
�E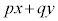 �́A
�́A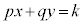 �Ƃ����āAk�����܂�(�����͕��s�ړ����܂�)�B
�Ƃ����āAk�����܂�(�����͕��s�ړ����܂�)�B �E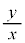 �́A
�́A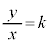 �Ƃ����āA�����F
�Ƃ����āA�����F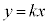 �̌X��k�����܂��B
�̌X��k�����܂��B �E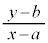 �́A
�́A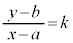 �Ƃ����āA�����F
�Ƃ����āA�����F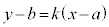 �̌X��k�����܂��B
�̌X��k�����܂��B �E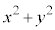 �́A
�́A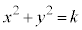 �Ƃ����āA���_�𒆐S�Ƃ���~�̔��a�����܂��B
�Ƃ����āA���_�𒆐S�Ƃ���~�̔��a�����܂��B x�Cy���̈�D���̓_�ł���A�Ƃ��������̉��ɁA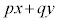 �C
�C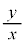 �C
�C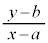 �C
�C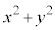 �̍ő�l�A�ŏ��l�����߂���ł���Ak�����Ē����A�~�����A�̈�D��ʉ߂��钼���A���邢�͉~�̒���k���ő�ɂȂ���́Ak���ŏ��ɂȂ���̂����߂�A���̂Ƃ���k�����߂�ő�l�A�ŏ��l�ł��B
�̍ő�l�A�ŏ��l�����߂���ł���Ak�����Ē����A�~�����A�̈�D��ʉ߂��钼���A���邢�͉~�̒���k���ő�ɂȂ���́Ak���ŏ��ɂȂ���̂����߂�A���̂Ƃ���k�����߂�ő�l�A�ŏ��l�ł��B
���@���iX��1g��������̂ɁA�ޗ�1��4g�C�ޗ�2��1g�C�ޗ�3��4g�g���A���iY��1g��������̂ɁA�ޗ�1��1g�C�ޗ�2��3g�C�ޗ�3��3g�g���B�ޗ�1�͑S����24kg�C�ޗ�2�͑S����18kg�C�ޗ�3�͑S����27kg����B���iX�CY�̉��i��1g������A���ꂼ��A10�~�C20�~�Ƃ���Ƃ��A�ł�����グ�𑝂₷���߂ɂ́A���iX�CY�����ꂼ�ꉽkg����������ׂ����B���iX�CY�̉��i��1g������20�~�C10�~�̂Ƃ��͂ǂ����B�����������̂͂��ׂĔ������̂Ƃ���B
���@���iX�CY�����ꂼ��Axkg�Cykg��������Ƃ��܂��B
���iX��xkg��������̂ɁA�ޗ�1��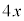 kg�C�ޗ�2��
kg�C�ޗ�2��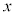 kg�C�ޗ�3��
kg�C�ޗ�3��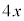 kg�g���܂��B
kg�g���܂��B
���iY��ykg��������̂ɁA�ޗ�1��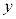 kg�C�ޗ�2��
kg�C�ޗ�2��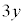 kg�C�ޗ�3��
kg�C�ޗ�3��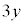 kg�g���܂��B
kg�g���܂��B
 �ޗ�1�Ɋւ�������́A
�ޗ�1�Ɋւ�������́A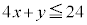 �@����@
�@����@
�ޗ�2�Ɋւ�������́A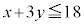 �@����A
�@����A
�ޗ�3�Ɋւ�������́A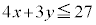 �@����B
�@����B
�܂��A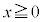 �C
�C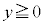 �ł��B
�ł��B
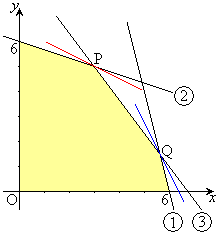
�����̏�����S�Ė�����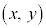 �́A�E�}�ʼn��F�ɓh��ꂽ�̈�(���E�����܂�)�ł��B
�́A�E�}�ʼn��F�ɓh��ꂽ�̈�(���E�����܂�)�ł��B
�A�ƇB�̋��E���̌�_P�����߂�ƁA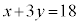 �C
�C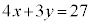 ��A�����A
��A�����A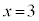 �C
�C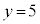
�@�ƇB�̋��E���̌�_Q�����߂�ƁA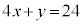 �C
�C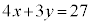 ��A�����A
��A�����A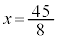 �C
�C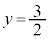
���iX�CY�̉��i��1g������10�~�C20�~�̂Ƃ��A����グ�́A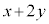 ���~�ł��B
���~�ł��B
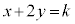 �Ƃ����ƁA�X����
�Ƃ����ƁA�X����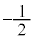 �̒�����\���܂��Bk�����Ē����s�ړ����Ak���ő�̂Ƃ����T���ƁA����
�̒�����\���܂��Bk�����Ē����s�ړ����Ak���ő�̂Ƃ����T���ƁA����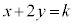 ���_P��ʂ�Ƃ�(�E�}�̐ԐF�̒���)�ł��B�_P�ɂ����ẮA
���_P��ʂ�Ƃ�(�E�}�̐ԐF�̒���)�ł��B�_P�ɂ����ẮA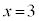 �C
�C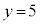 �Ȃ̂ŁA���iX��3kg�C���iY��5kg��������Ƃ��ɍő�̔���グ
�Ȃ̂ŁA���iX��3kg�C���iY��5kg��������Ƃ��ɍő�̔���グ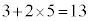 ���~�������܂��B
���~�������܂��B
���iX�F3kg�C���iY�F5kg ......[��]
���iX�CY�̉��i��1g������20�~�C10�~�̂Ƃ��A����グ�́A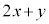 ���~�ł��B
���~�ł��B
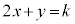 �Ƃ����ƁA�X����
�Ƃ����ƁA�X����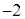 �̒�����\���܂��Bk�����Ē����s�ړ����Ak���ő�̂Ƃ����T���ƁA����
�̒�����\���܂��Bk�����Ē����s�ړ����Ak���ő�̂Ƃ����T���ƁA����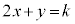 ���_Q��ʂ�Ƃ�(�E�}�̐F�̒���)�ł��B�_Q�ɂ����ẮA
���_Q��ʂ�Ƃ�(�E�}�̐F�̒���)�ł��B�_Q�ɂ����ẮA �C
�C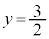 �Ȃ̂ŁA���iX��
�Ȃ̂ŁA���iX��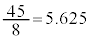 kg�C���iY��
kg�C���iY��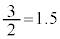 kg��������Ƃ��ɍő�̔���グ
kg��������Ƃ��ɍő�̔���グ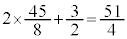 ���~�������܂��B
���~�������܂��B
���iX�F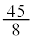 kg�C���iY�F
kg�C���iY�F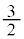 kg ......[��]
kg ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B