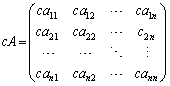行列 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
いくつかの数を長方形状に並べたものを行列と言う。
横の並びを1組にして行、縦の並びを1組にして列と言う。
行列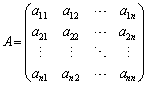 があるとき、
があるとき、
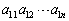 を第1行,
を第1行,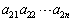 を第2行,
を第2行,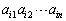 を第i行と言う。
を第i行と言う。
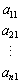 を第1列,
を第1列,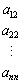 を第2列,
を第2列,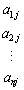 を第j列と言う。
を第j列と言う。
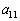 を行列の
を行列の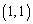 成分、
成分、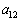 を
を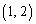 成分、
成分、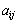 を
を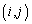 成分(i行目のj列目)と言う。
成分(i行目のj列目)と言う。
行の数m、列の数nの行列を、”m行n列の行列”,‘m×n行列'と言う。
とくに、n行n列の行列をn次正方行列と言う。
n次正方行列の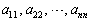 (行の番号と列の番号が同じ成分)を行列Aの対角成分と言う。
(行の番号と列の番号が同じ成分)を行列Aの対角成分と言う。
n次正方行列の対角成分が全て1,他は全て0になる行列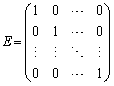 をn次単位行列と言う。
をn次単位行列と言う。
成分が全て0の行列を零行列と言い、O (大文字のオー)で表す。
行列Aの第i行を第i列にしてできる行列(行と列を入れ替えた行列)
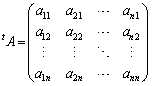 をAの転置行列という。
をAの転置行列という。
1行のみの行列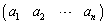 を行ベクトル、1列のみの行列
を行ベクトル、1列のみの行列 を列ベクトルと言う。
を列ベクトルと言う。
行列を、行ベクトルを縦に並べたもの、列ベクトルを横に並べたものとして扱うことがある。
このウェブサイトでは、行列を扱うとき、単に”ベクトル”と呼ぶときは縦ベクトル(縦に数字を並べたベクトル)を表すものとする。
また、縦ベクトルを横ベクトルに直すときには転置記号を使うことにする。つまり、
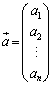 とするとき、
とするとき、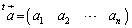 と書くことにする。
と書くことにする。
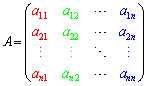 ,
,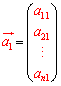 ,
,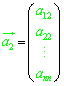 ,・・・,
,・・・,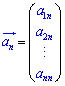 とすれば、
とすれば、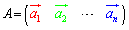 のように表せる。
のように表せる。
 ,
,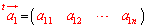 ,
, ,・・・,
,・・・,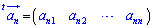 とすれば、
とすれば、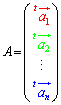 のように表せる。つまり、行ベクトルを、その行の成分を一旦縦ベクトルの形に書いて転置したものとして考える。
のように表せる。つまり、行ベクトルを、その行の成分を一旦縦ベクトルの形に書いて転置したものとして考える。
例1.(1) 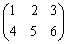 は2行3列の行列。
は2行3列の行列。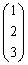 は3行1列の行列(または3次元列ベクトル)。
は3行1列の行列(または3次元列ベクトル)。
(2) 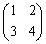 は2次の正方行列,
は2次の正方行列,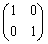 は2次の単位行列。
は2次の単位行列。
(3) 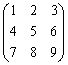 は3次の正方行列,
は3次の正方行列,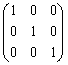 は3次の単位行列。
は3次の単位行列。
例2. 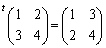 ,
,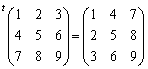
行列の和と差: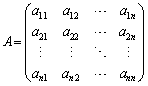 ,
,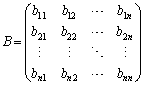 として、
として、
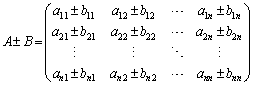 (複号同順)
(複号同順)
行列の実数倍(スカラー倍):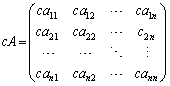
Aの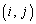 成分を
成分を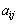 ,Bの
,Bの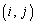 成分を
成分を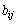 として(
として(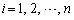 ,
,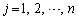 )、
)、
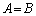 ⇔
⇔ 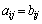 (すべてのi,jに対して)
(すべてのi,jに対して)
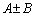 の
の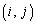 成分は、
成分は、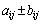 (同一成分どうしで和と差をとればよい)
(同一成分どうしで和と差をとればよい)
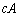 の
の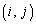 成分は、
成分は、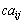 (全ての成分に実数cをかける)
(全ての成分に実数cをかける)
例3. 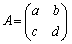 ,
,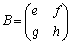 として、
として、
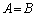 ⇔
⇔ 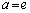 かつ
かつ 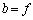 かつ
かつ 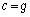 かつ
かつ 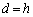
例4. 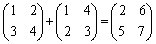 ,
,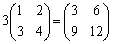 ,
,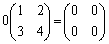 (零行列)
(零行列)
2つの同型の行列A,Bの和について、
交換法則: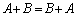
結合法則: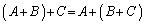
が成立する。また、
 ,
,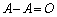
行列の実数倍について、
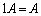 ,
,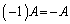 ,
,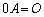 ,
,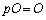 (p:実数)
(p:実数)
p,qを実数,A,Bを同型の行列として、
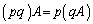 ,
,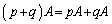 ,
,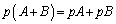
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 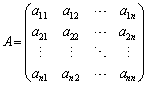 があるとき、
があるとき、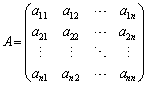 があるとき、
があるとき、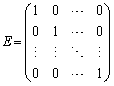 をn次単位行列と言う。
をn次単位行列と言う。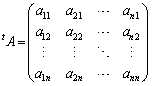 をAの転置行列という。
をAの転置行列という。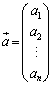 とするとき、
とするとき、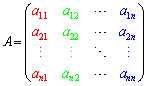 ,
,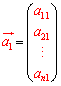 ,
,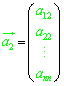 ,・・・,
,・・・,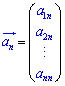 とすれば、
とすれば、 ,
, のように表せる。つまり、行ベクトルを、その行の成分を一旦縦ベクトルの形に書いて転置したものとして考える。
のように表せる。つまり、行ベクトルを、その行の成分を一旦縦ベクトルの形に書いて転置したものとして考える。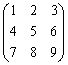 は3次の正方行列,
は3次の正方行列,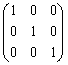 は3次の単位行列。
は3次の単位行列。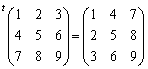
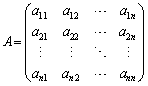 ,
,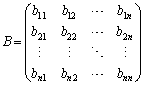 として、
として、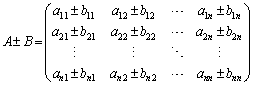 (複号同順)
(複号同順)