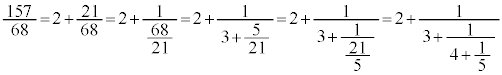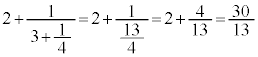Euclid�̌ݏ��@�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
1529388��419832�̍ő�������߂�B�Ƃ������ɑ��Ď��̂悤�ȉ�@���m���Ă��܂��B
(i) �傫�����̐������������̐��Ŋ���B
1529388��419832��3���܂�269892
(ii) (i)�̊��鐔��(i)�̗]��Ŋ���B
419832��269892��1���܂�149980
(iii) (ii)�̊��鐔��(ii)�̂��܂�Ŋ���B
269892��149980��1���܂�119952
(iv) (iii)�̊��鐔��(iii)�̂��܂�Ŋ���B
149980��119952��1���܂�29980
(v) (iv)�̊��鐔��(iv)�̂��܂�Ŋ���B
119952��29980��4���܂�0
����ŁA1529388��419832�̍ő����29988�ł��邱�Ƃ��킩��܂��B
���ہA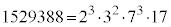 �C
�C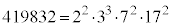 �C
�C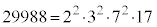 �ł��B�ɑ傫�ȑf�����܂ޏꍇ�A�f����������������Ƃ�����܂����A��L�̉�@�ł͗e�Ղɍő�������߂邱�Ƃ��ł��܂��B���̉�@��(���[�N���b�h��)�ݏ��@�ƌ����܂��B
�ł��B�ɑ傫�ȑf�����܂ޏꍇ�A�f����������������Ƃ�����܂����A��L�̉�@�ł͗e�Ղɍő�������߂邱�Ƃ��ł��܂��B���̉�@��(���[�N���b�h��)�ݏ��@�ƌ����܂��B
2��a�Cb (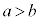 )������Ƃ��Aa��b�Ŋ����ď���s�C���܂肪r���Ƃ��܂��B
)������Ƃ��Aa��b�Ŋ����ď���s�C���܂肪r���Ƃ��܂��B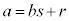 �ł��B
�ł��B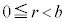 �ł��B�@(��)
�ł��B�@(��)
���ɁA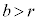 �Ȃ̂ŁA(��)��a��b�ɁCb��r�ɂ��āA(��)���J��Ԃ��܂��B
�Ȃ̂ŁA(��)��a��b�ɁCb��r�ɂ��āA(��)���J��Ԃ��܂��B
�J��Ԃ��ɂ�āAa�Cb�Cr�͎���ɏ������Ȃ�A�L�����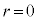 �ɂȂ�܂��B
�ɂȂ�܂��B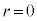 �ɂȂ����Ƃ���b���ő���ł��B
�ɂȂ����Ƃ���b���ő���ł��B
a�Cb�̍ő����m�Ƃ��܂��B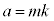 �C
�C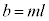 �ƂȂ�݂��ɑf�Ȑ����̑gk�Cl�����݂��܂��B
�ƂȂ�݂��ɑf�Ȑ����̑gk�Cl�����݂��܂��B
 ���A
���A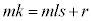 �@��
�@�� 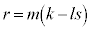
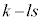 �͐����Ȃ̂ŁAr��m�̔{���ł��B
�͐����Ȃ̂ŁAr��m�̔{���ł��B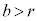 �Ȃ̂ŁAm��b�Cr�̍ő���ł�(m�����傫�ȍő��������Ƃ���Am��a�Cb�̍ő���ɂȂ�܂���)�B
�Ȃ̂ŁAm��b�Cr�̍ő���ł�(m�����傫�ȍő��������Ƃ���Am��a�Cb�̍ő���ɂȂ�܂���)�B
(��)���J��Ԃ��ƁA�e���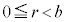 �ł��邽�߁A(��)��a�Cb�Cr�͂ǂ�ǂ����Ȃ�A�L����(��)���J��Ԃ����Ƃ���ōŏI���m�̔{��a��
�ł��邽�߁A(��)��a�Cb�Cr�͂ǂ�ǂ����Ȃ�A�L����(��)���J��Ԃ����Ƃ���ōŏI���m�̔{��a��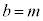 �Ŋ���A������̂�
�Ŋ���A������̂�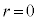 �ƂȂ�܂��B
�ƂȂ�܂��B
���[�N���b�h�̌ݏ��@��157��68�̍ő�������߂Ă݂܂��B
157��68��2���܂�21�@����@
68��21��3���܂�5�@����A
21��5��4���܂�1�@����B
5��1��5���܂�0
�ƂȂ�A�ő����1�ɂȂ�܂��B�܂�A157��68�݂͌��f�A�Ƃ������Ƃł��B
�B���A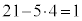 �@����C
�@����C
�A���A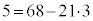 �C������C�ɑ������ƁA
�C������C�ɑ������ƁA
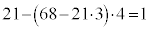
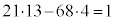 �@����D
�@����D
�@���A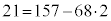 �C������D�ɑ������ƁA
�C������D�ɑ������ƁA
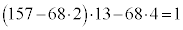
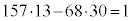
������A�s��������F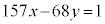 �̓�������A
�̓�������A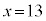 �C
�C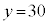 �Ƌ��߂邱�Ƃ��ł��܂��B
�Ƌ��߂邱�Ƃ��ł��܂��B
a�Cb���݂��ɑf(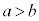 �Ƃ��܂�)�ȂƂ��A�s��������F
�Ƃ��܂�)�ȂƂ��A�s��������F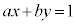 �̓�������ݏ��@��p���ċ��߂邱�Ƃ��ł��܂��B
�̓�������ݏ��@��p���ċ��߂邱�Ƃ��ł��܂��B
�ݏ��@���J��Ԃ��āAm��n�Ŋ����Ă��܂肪1�ɂȂ����Ƃ��A����s���Ƃ��āA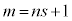 �C
�C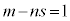
�����Ōݏ��@�̓r���o�߂�m�Cn�ɏ���������Ă䂫�Aa�Cb���o�Ă���܂ŌJ��Ԃ��A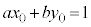 �̌`�ɂȂ����Ƃ���ŁA�����
�̌`�ɂȂ����Ƃ���ŁA�����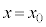 �C
�C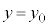 �������܂��B
�������܂��B
�Ȃ��A�ݏ��@���ʓ|�ȏꍇ�A�A�����W�J�A�Ƃ����ȕւȕ��@���m���Ă��܂��B���嗝�H93�N[1]�ɏo�肳��܂������A
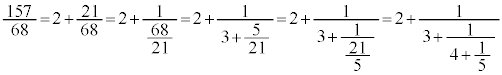
�̂悤�ɁA�A�����ŕ\���Ȃ���A�o�Ă��������̋t��������ĕ��q��1�ɂ��Ă䂫�A���q��1���o�Ă���܂ő����܂��B���̑���͌ݏ��@�Ɠ������̂ł��B�����ŁA��ԓ����ɏo�Ă���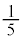 ���������A���������ɖ߂��Ă䂫�܂��B
���������A���������ɖ߂��Ă䂫�܂��B
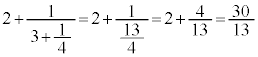
���̂Ƃ��ɏo�Ă���30��13�����̕s��������̓�����ɂȂ��Ă��܂��B�ڂ����́A���ؒ厡���u���������_�u�`�vp.129�Cp.130���Q�Ƃ��Ă��������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B