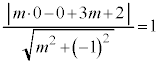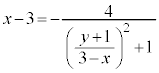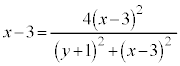円の媒介変数表示 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
円: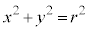 (
(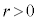 )上の点P
)上の点P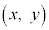 は、円とx軸との交点をA,
は、円とx軸との交点をA,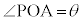 として、
として、
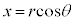 ,
,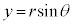 ・・・①
・・・①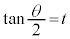 として、
として、
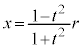 ,
,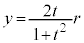 ・・・②
・・・②
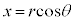 ,
,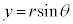 のとき、
のとき、
より、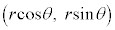 は、円:
は、円: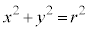 上の点です。同様に、
上の点です。同様に、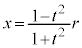 ,
,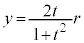 のとき、
のとき、
より、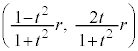 は、円:
は、円: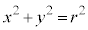 上の点です。
上の点です。
例1.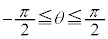 となるθについて、
となるθについて、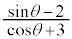 の最大値、最小値を求める。
の最大値、最小値を求める。
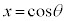 ,
,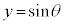 とおくと、点
とおくと、点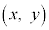 は、
は、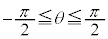 より、円:
より、円: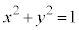 の
の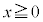 の部分の半円上の点です。このとき、
の部分の半円上の点です。このとき、
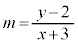 ・・・③
・・・③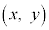 と
と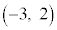 を結ぶ直線の傾きです。傾きmが最小になるのは、直線が円上の点
を結ぶ直線の傾きです。傾きmが最小になるのは、直線が円上の点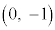 を通るときで、③に
を通るときで、③に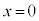 ,
,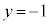 を代入して、mの最小値は、
を代入して、mの最小値は、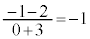
傾きmが最大になるのは、直線が円と第1象限で接するときで、直線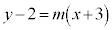 ,即ち、
,即ち、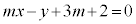 と、円の中心
と、円の中心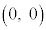 との距離が円の半径1に等しいとおいて、
との距離が円の半径1に等しいとおいて、
分母を払い、2乗して、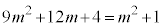
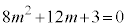 ∴
∴ 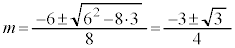
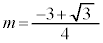 ,これが最大値です。
,これが最大値です。
例2.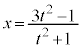 ・・・④,
・・・④,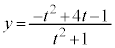 ・・・⑤ と媒介変数表示される曲線がある。ここから媒介変数tを消去してx,yの方程式を作る。
・・・⑤ と媒介変数表示される曲線がある。ここから媒介変数tを消去してx,yの方程式を作る。
まず、④,⑤の分数式において、分子の次数が分母の次数よりも小さくなるようにします。
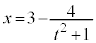 ・・・⑥,
・・・⑥,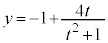 ・・・⑦
・・・⑦
⑥より、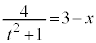 ,⑦に代入すると、
,⑦に代入すると、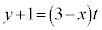
∴ 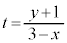 (
(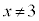 )
)
これを⑥に代入すれば、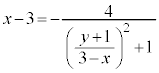
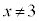 として、
として、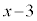 を約し、分母を払うと、
を約し、分母を払うと、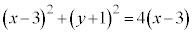
展開して整理すると、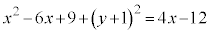
∴ 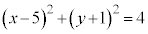
なお、⑥において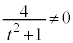 より、
より、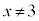 です。
です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 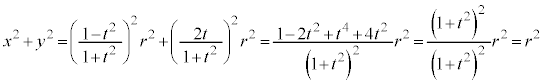
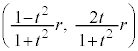 は、円:
は、円: