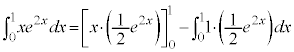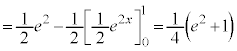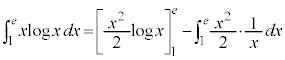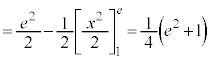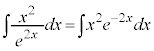�����ϕ��@�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�����F
[�ؖ�]�@�ς̔����@�̌����F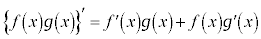 ���A
���A
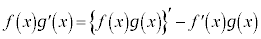
���ӂ�x�Őϕ�����ƁA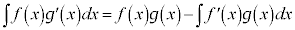 �@(�ؖ��I)
�@(�ؖ��I)
��ϕ��̏ꍇ�ɂ́A
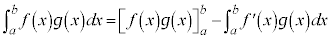
�ƂȂ�܂��B
�����ϕ��@�ł́A��ϕ�����2�̍��̐ςƌ��āA�Е���������A�Е���ϕ����邱�ƂɂȂ�܂��B
�ϕ����邱�Ƃɂ�������(�����ł́A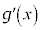 )���ɐϕ����āA
)���ɐϕ����āA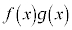 �Ƃ������������܂��B
�Ƃ������������܂��B
���ɁA�}�C�i�X�����āA�������邱�Ƃɂ�������(�����ł́A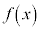 )��������A
)��������A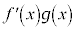 �̐ϕ��������܂��B
�̐ϕ��������܂��B
��1�D�@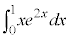
x�͔��������1�ƂȂ�A�ȒP�ɂȂ�̂ŁAx��������A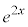 ��ϕ����܂��B
��ϕ����܂��B
��L�̌����ɂ��Ă͂߂�ƁA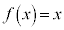 �C
�C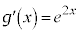 �Ƃ��܂��B
�Ƃ��܂��B
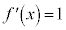 �C
�C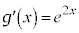 ��ϕ�����
��ϕ�����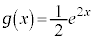 �ł��B����āA
�ł��B����āA
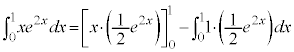
�@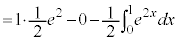
�@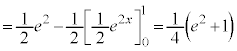
��2�D�@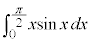
��1�Ɠ��l��x�͔��������1�ƂȂ�A�ȒP�ɂȂ�̂ŁAx��������A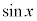 ��ϕ����܂��B
��ϕ����܂��B
��L�̌����ɂ��Ă͂߂�ƁA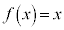 �C
�C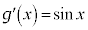 �Ƃ��܂��B
�Ƃ��܂��B
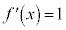 �C
�C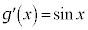 ��ϕ�����
��ϕ�����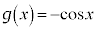 �ł��B����āA
�ł��B����āA
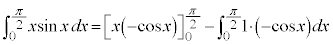
�@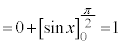
��3�D�@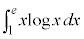
x���������ƁA ��ϕ����邱�ƂɂȂ��Ă��܂��̂ł����A
��ϕ����邱�ƂɂȂ��Ă��܂��̂ł����A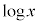 �̐ϕ���
�̐ϕ���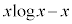 �Ō��NJȒP�ɂȂ�܂���B
�Ō��NJȒP�ɂȂ�܂���B
�����ŁA�ΐ������o�Ă���ꍇ�ɂ́A�ΐ����̕���������܂��Bx�͐ϕ����邱�ƂɂȂ�܂��B
��L�̌����ɂ��Ă͂߂�ƁA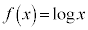 �C
�C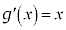 �Ƃ��܂��B
�Ƃ��܂��B
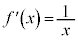 �C
�C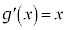 ��ϕ�����
��ϕ�����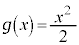 �ł��B����āA
�ł��B����āA
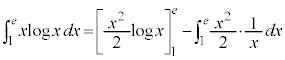
�@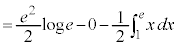
�@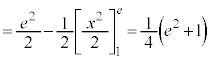
��4�D�@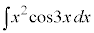
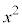 ������A
������A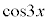 ��ϕ����܂��B�����ϕ���1��s�������ł́A
��ϕ����܂��B�����ϕ���1��s�������ł́A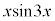 �̐ϕ����c��܂����A����ɁAx������A
�̐ϕ����c��܂����A����ɁAx������A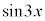 ��ϕ��ɂ��ĕ����ϕ����邱�ƂŁA�v�Z���I�����܂��B
��ϕ��ɂ��ĕ����ϕ����邱�ƂŁA�v�Z���I�����܂��B
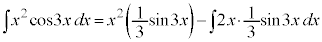
�@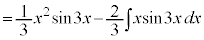
�@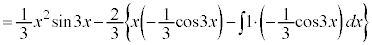
�@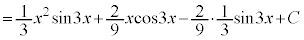
�@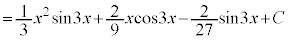 (C�F�ϕ��萔)
(C�F�ϕ��萔)
��5�D�@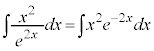
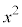 ������A
������A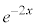 ��ϕ����܂��B�����ϕ���1��s�������ł́A
��ϕ����܂��B�����ϕ���1��s�������ł́A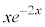 �̐ϕ����c��܂����A����ɁAx������A
�̐ϕ����c��܂����A����ɁAx������A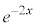 ��ϕ��ɂ��ĕ����ϕ����邱�ƂŁA�v�Z���I�����܂��B
��ϕ��ɂ��ĕ����ϕ����邱�ƂŁA�v�Z���I�����܂��B
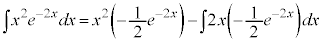
�@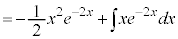
�@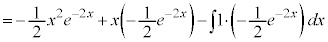
�@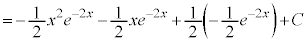
�@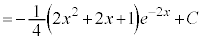 (C�F�ϕ��萔)
(C�F�ϕ��萔)
[�ʉ�]�@�Ȃ��A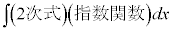 �Ƃ����ϕ��̏ꍇ�ɂ́A�s��ϕ���
�Ƃ����ϕ��̏ꍇ�ɂ́A�s��ϕ��� �̌`�ɂȂ�̂ŁA�ȉ��̂悤�Ɍv�Z����������N�ɂ��݂܂��B�����ϕ��͌v�Z���~�X���₷���̂ŁA�������ŕ����ϕ�������邱�Ƃ��\�Ȃ�A�ɗ͔�����ׂ��ł��B
�̌`�ɂȂ�̂ŁA�ȉ��̂悤�Ɍv�Z����������N�ɂ��݂܂��B�����ϕ��͌v�Z���~�X���₷���̂ŁA�������ŕ����ϕ�������邱�Ƃ��\�Ȃ�A�ɗ͔�����ׂ��ł��B
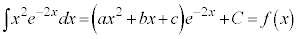 �Ƃ����܂��B
�Ƃ����܂��B
�E�ӂ�x�Ŕ�������ƁA
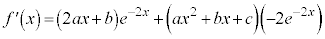
�@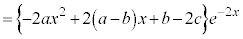 �@����@
�@����@
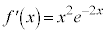 �@����A�@���A
�@����A�@���A
�@�C�A���ŌW����r���āA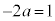 �C
�C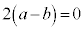 �C
�C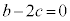
�����������āA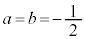 �C
�C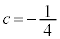
�� 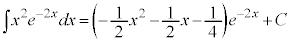 (C�F�ϕ��萔)
(C�F�ϕ��萔)
��6�D�@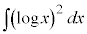
��ϕ������ΐ������܂ފ������̏ꍇ�́A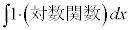 �ƌ��āA1��ϕ����A
�ƌ��āA1��ϕ����A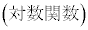 ��������āA�����ϕ����s���܂��B
��������āA�����ϕ����s���܂��B
�����ł́A1���ϕ����Ă��A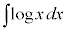 ���c��̂ł����A����́A�����F
���c��̂ł����A����́A�����F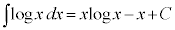 ���g���܂��B
���g���܂��B
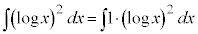
�@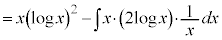
�@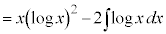
�@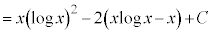
�@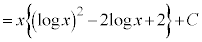 �@(C�F�ϕ��萔)
�@(C�F�ϕ��萔)
��7�D�@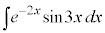
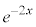 ��ϕ��ɉĂ��A
��ϕ��ɉĂ��A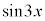 ��ϕ��ɉĂ��A�J�͓͂����ł��B�����ł́A
��ϕ��ɉĂ��A�J�͓͂����ł��B�����ł́A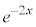 ��ϕ��ɉ��j�ł���Ă݂܂��B
��ϕ��ɉ��j�ł���Ă݂܂��B
2���ϕ�����Ƃ͂��߂Ɠ����`���o�Ă���̂ŁA�ŏ��̌`��I�Ƃ����āA
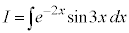
�@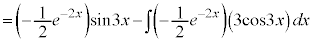
�@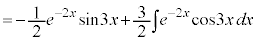
�@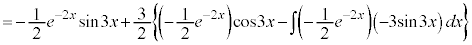
�@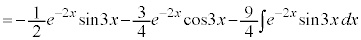
�@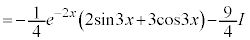 �@(�ŏ��̌`���o�Ă���̂ŁA�����I�Ƃ���)
�@(�ŏ��̌`���o�Ă���̂ŁA�����I�Ƃ���)
�� 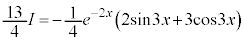
�� 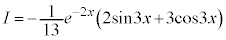
�� 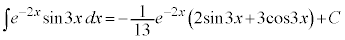 �@(C�F�ϕ��萔)
�@(C�F�ϕ��萔)
[�ʉ�]�@���̐ϕ�����5�D�Ɠ��l�ɁA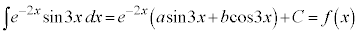 �Ƃ����āA
�Ƃ����āA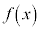 ��������ČW����r���邱�Ƃɂ���āA�s��ϕ������߂���@���l�����܂��B
��������ČW����r���邱�Ƃɂ���āA�s��ϕ������߂���@���l�����܂��B
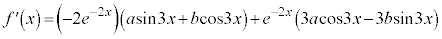
�@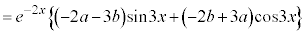
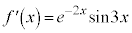 �ƌW����r���āA
�ƌW����r���āA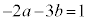 �C
�C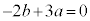
�����������āA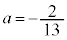 �C
�C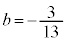
�� 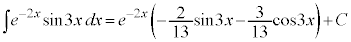 �@(C�F�ϕ��萔)
�@(C�F�ϕ��萔)
���D��4�D�`��7�D��s��ϕ��ŗᎦ���܂������A��ϕ��ɂ����Ă��A�s��ϕ����ϕ��ɂ����A�ϕ��̂��Ȃ����́A �Ƃ���A���l�Ɍv�Z���s���܂��B
�Ƃ���A���l�Ɍv�Z���s���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B