順列 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
1から自然数をnまで順にかけあわせたものをnの階乗と言い、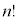 と表す。
と表す。
順序をつけて1列に並べたものを順列と言う。異なるn個のものからr個を選んで1列に並べる順列の総数を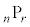 と表す。
と表す。
公式: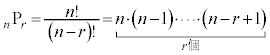
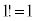 ,
,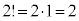 ,
,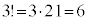 ,
,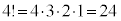 ,
,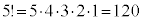 ,・・・,
,・・・,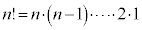 です。
です。
特別に、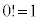 と定めます。
と定めます。
白、赤、緑、黄、青の5色に塗り分けられたボールから3個を選んで1列に並べる方法は、最初の1個の選び方が5通り、仮に白を選んだとして、2個めの選び方は残り4個から選ぶので4通り、3個めの選び方は残り3個から選ぶので3通りで、
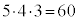 通りになります。
通りになります。
n個の異なるボールからr個を選んで1列に並べる方法は、同様に考えて、最初の1個がn通り、2個目が残りの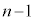 通り、・・・、r個目が
通り、・・・、r個目が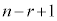 通りで、
通りで、
 通りです。
通りです。
これは、また、階乗の記号を使って、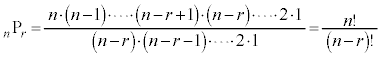 と書けます。
と書けます。
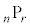 は、nから始まって1ずつ減りながら
は、nから始まって1ずつ減りながら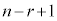 まで連続r個の整数の積です。
まで連続r個の整数の積です。
5個の異なるものから3個を選んで1列に並べるときには、順列の公式より、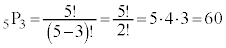 通りとなります。
通りとなります。
n個の異なるものからn個全部を選んで1列に並べる方法の数は、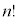 通りです。
通りです。
必ずしも並べるような場合でなくても、順列の考え方が使えます。
例えば、8人の人で委員会を構成するときに、委員長と書記と会計の3人の役員の割り当て方は何通りあるか、という問題は、異なる8つのものから3個のものを選んで1列に並べるのと同等に考えることができて、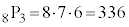 通りです。
通りです。
また、8脚の異なる椅子があって、そこにA君、B君、C君の3人が座るとき、座り方が何通りあるか、という問題も、やはり、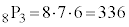 通りです。
通りです。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 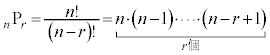
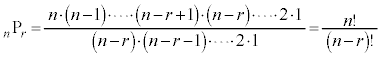 と書けます。
と書けます。