同じものを含む順列 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
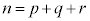 として、文字aをp個、文字bをq個、文字cをr個、一列に並べて作ることのできる順列の個数は、
として、文字aをp個、文字bをq個、文字cをr個、一列に並べて作ることのできる順列の個数は、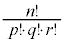 個
個
まず、文字を置くn個の位置からaを置くp個の位置を選ぶのが、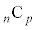 通り、残った
通り、残った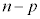 個の位置からbを置くq個の位置を選ぶのが、
個の位置からbを置くq個の位置を選ぶのが、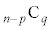 通り。これで、cを置く位置も確定します。順列の個数は、
通り。これで、cを置く位置も確定します。順列の個数は、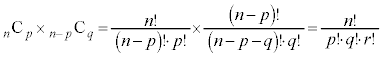 個(注.
個(注.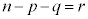 )です。
)です。
また、n個の異なるものを並べる並べ方が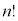 通りあって、p個の文字aがすべて異なるとしてその並べ方が
通りあって、p個の文字aがすべて異なるとしてその並べ方が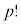 通り、q個の文字bがすべて異なるとしてその並べ方が
通り、q個の文字bがすべて異なるとしてその並べ方が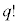 通り、r個の文字cがすべて異なるとしてその並べ方が
通り、r個の文字cがすべて異なるとしてその並べ方が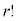 通りあり、実際には、文字a同士の
通りあり、実際には、文字a同士の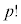 通りの並べ替え、文字b同士の
通りの並べ替え、文字b同士の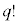 通りの並べ替え、文字c同士の
通りの並べ替え、文字c同士の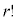 通りの並べ替えを区別できないので、順列の個数は、
通りの並べ替えを区別できないので、順列の個数は、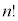 を
を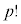 ,
,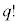 ,
,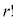 で割って、
で割って、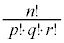 個、という求め方もできます。
個、という求め方もできます。
3種類以上の文字がある場合についても、全く同様の関係式:総個数の階乗をそれぞれの文字の文字数の階乗の積で割ったもの、になります。
例.(1) 数字1を3個、数字2を2個、数字3を5個使ってできる10桁の整数は、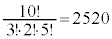 通りできます。
通りできます。
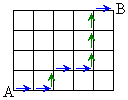 (2) 右図のような碁盤目上の道路を最短経路でAからBまで行く経路の数を考えます。
(2) 右図のような碁盤目上の道路を最短経路でAからBまで行く経路の数を考えます。
AからBまで、例えば右図の矢印のような経路では、右−右−上−右−右−上−上−上−右、と進むことによりAからBまで行くことができます。これを見ると、右に5回、上に4回進むと、AからBに到達できることが分かります。‘上'と‘右'の並び方を変えると異なる経路になります。
従って、‘右'5文字と‘上'4文字を一列に並べる順列と考えることにより、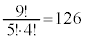 通りの経路があります。
通りの経路があります。
(3) 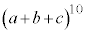 を展開したときの
を展開したときの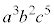 の係数を考えます。
の係数を考えます。
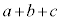 を10回かけて展開するとき、それぞれの
を10回かけて展開するとき、それぞれの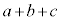 のa,b,cのどれを選んで10回かけていくかと考えると、
のa,b,cのどれを選んで10回かけていくかと考えると、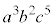 では、aを3回、bを2回、cを5回選んでかけることになります。
では、aを3回、bを2回、cを5回選んでかけることになります。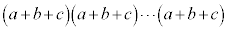 とかけ合わされている10個の
とかけ合わされている10個の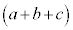 のどの3個からa,どの2個からb,どの5個からcをとってかけ合わせるか、ということで
のどの3個からa,どの2個からb,どの5個からcをとってかけ合わせるか、ということで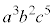 という項の個数が決まります。従って、
という項の個数が決まります。従って、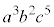 の係数を、文字aを3個、文字bを2個、文字cを5個、一列に並べる順列の個数として求めると、
の係数を、文字aを3個、文字bを2個、文字cを5個、一列に並べる順列の個数として求めると、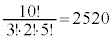 となります。
となります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 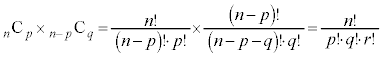 個(注.
個(注.